题目内容
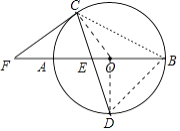
【题目】如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF. 
(1)求证:CF与⊙O相切;
(2)若DEDC=13,求⊙O的半径.
【答案】
(1)解:连接OC、OD.
∵ ![]() =
= ![]() ,
,
∴OD⊥AB,∠AOD=90°,
∵FE=FC,
∴∠FCE=∠FEC,
∵OC=OD,
∴∠OCE=∠ODC,
∴∠FCO=∠FCE+∠OCE=∠FEC+∠EDO=∠OED+∠ODC=90°.
∴OC⊥CF,
∴CF是⊙⊙O的切线
(2)解:连接BC、BD.

∵ ![]() =
= ![]() ,
,
∠EBD=∠BCD,
∵∠BDE=∠CDB,
∴△BDE∽△CDB,
∴ ![]() =
= ![]() ,
,
∴BD2=CDED=13,
∵∠BOD=90°,
∴OB2+OD2=BD2=13,
∴OB2= ![]() ,
,
∴OB= ![]() ,
,
∴⊙O的半径为 ![]()
【解析】(1)欲证明CF与⊙O相切,只要证明OC⊥CF即可.(2)由△BDE∽△CDB,推出 ![]() =
= ![]() ,推出BD2=CDED=12,由∠BOD=90°,推出OB2+OD2=BD2=12,推出OB2=6,可得OB=
,推出BD2=CDED=12,由∠BOD=90°,推出OB2+OD2=BD2=12,推出OB2=6,可得OB= ![]() 解决问题.
解决问题.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目