Question

在Rt△ABC中，∠A＜∠B，CM是斜边AB上的中线，将△ACM沿直线CM折叠，点A落在点D处，如果CD恰好与AB垂直，那么∠A的度数是（ ）

A．15°
B．30°
C．45°
D．60°

Answer 1

【答案】分析：根据折叠的性质可知，折叠前后的两个三角形全等，则∠D=∠A，∠MCD=∠MCA，再由直角三角形斜边中线的性质可得出∠MCD=∠D，从而求得∠A的度数．
解答：解：在直角△ABC中，CM=AM=MB，（直角三角形的斜边中线等于斜边一半），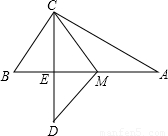
∴∠A=∠ACM，
由折叠的性质可得：∠A=∠D，∠MCD=∠MCA，AM=DM，
∴MC=MD，∠A=∠ACM=∠MCE，
∵AB⊥CD，
∴∠CMB=∠DMB，∠CEB=∠MED=90°，
∵∠B+∠A=90°，∠B+∠ECB=90°，
∴∠A=∠ECB，
∴∠A=∠ACM=∠MCE=∠ECB，
∴∠A=∠ACB=30°，
故选B．
点评：本题考查图形的折叠变化及三角形的内角和定理．关键是要理解折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，只是位置变化．