ЬтФПФкШн
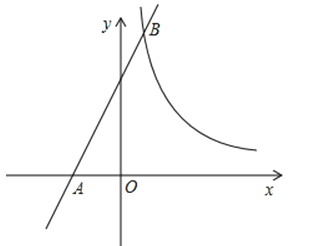
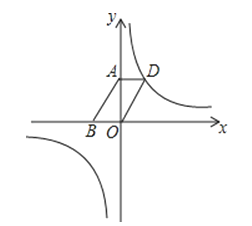
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЈ20ЃЌ0ЃЉЃЌвдOAЮЊжБОЖдкЕквЛЯѓЯоФкзїАыдВCЃЌЕуBЪЧИУАыдВжмЩЯвЛЖЏЕуЃЌСЌНсOBЁЂABЃЌВЂбгГЄABжСЕуDЃЌЪЙDB=ABЃЌЙ§ЕуDзїxжсДЙЯпЃЌЗжБ№НЛxжсЁЂжБЯпOBгкЕуEЁЂFЃЌЕуEЮЊДЙзуЃЌСЌНсCFЃЎ
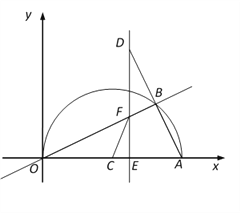
ЃЈ1ЃЉЕБЁЯAOB=30ЁуЪБЃЌЧѓЛЁOBЕФГЄЖШЃЛ
ЃЈ2ЃЉЕБDE=16ЪБЃЌЧѓЯпЖЮEFЕФГЄЃЛ
ЃЈ3ЃЉдкЕуBдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдквдЕуEЁЂCЁЂFЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЃЌШєДцдкЃЌЧыЧѓГіДЫ
ЪБЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ;ЃЈ2ЃЉ6Лђ24;ЃЈ3ЃЉEЕуЮЊ
;ЃЈ2ЃЉ6Лђ24;ЃЈ3ЃЉEЕуЮЊ![]()
ЁОНтЮіЁПЪдЬтЗжЮі: ЃЈ1ЃЉСЌНгBCЃЌгЩвбжЊЕУЁЯACB=2ЁЯAOB=60ЁуЃЌAC=![]() AO=10ЃЌИљОнЛЁГЄЙЋЪНЧѓНтЃЛ
AO=10ЃЌИљОнЛЁГЄЙЋЪНЧѓНтЃЛ
ЃЈ2ЃЉСЌНгODЃЌгЩДЙжБЦНЗжЯпЕФаджЪЕУOD=OA=20ЃЌгжDE=16ЃЌдкRtЁїODEжаЃЌгЩЙДЙЩЖЈРэЧѓOEЃЌвРЬтвтжЄУїЁїOEFЁзЁїDEAЃЌРћгУЯрЫЦБШЧѓEFЃЛ
ЃЈ3ЃЉДцдкЃЎЕБвдЕуEЁЂCЁЂFЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЪБЃЌЗжЮЊЂйЕБНЛЕуEдкOЃЌCжЎМфЪБЃЌгЩвдЕуEЁЂCЁЂFЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЃЌгаЁЯECF=ЁЯBOAЛђЁЯECF=ЁЯOABЃЌЂкЕБНЛЕуEдкЕуCЕФгвВрЪБЃЌвЊЪЙЁїECFгыЁїBAOЯрЫЦЃЌжЛФмЪЙЁЯECF=ЁЯBAOЃЌЂлЕБНЛЕуEдкЕуOЕФзѓВрЪБЃЌвЊЪЙЁїECFгыЁїBAOЯрЫЦЃЌжЛФмЪЙЁЯECF=ЁЯBAOЃЌШ§жжЧщПіЃЌЗжБ№ЧѓEЕузјБъЃЎ
ЪдЬтНтЮі: (1)СЌНгBC,
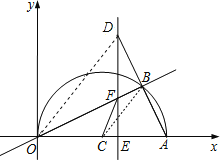
ЁпA(20,0)ЃЌЁрOA=20ЃЌCA=10ЃЌ
ЁпЁЯAOB=30ЁуЃЌ
ЁрЁЯACB=2ЁЯAOB=60ЁуЃЌ
ЁрЛЁABЕФГЄ=![]() =
=![]() ЃЛ
ЃЛ
(2)ЂйШєDдкЕквЛЯѓЯоЃЌ
СЌНгODЃЌ
ЁпOAЪЧЁбCжБОЖ,
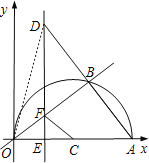
ЁрЁЯOBA=90ЁуЃЌ
гжЁпAB=BDЃЌ
ЁрOBЪЧADЕФДЙжБЦНЗжЯпЃЌ
ЁрOD=OA=20ЃЌ
дкRtЁїODEжаЃЌ
OE=![]() =
=![]() ЃЌ
ЃЌ
ЁрAE=AOOE=2012=8ЃЌ
гЩЁЯAOB=ЁЯADE=90ЁуЁЯOABЃЌЁЯOEF=ЁЯDEAЃЌ
ЕУЁїOEFЁзЁїDEAЃЌ
Ёр![]() ,МД
,МД![]() ЃЌ
ЃЌ
ЁрEF=6ЃЛ
ЂкШєDдкЕкЖўЯѓЯоЃЌ
СЌНгOD,
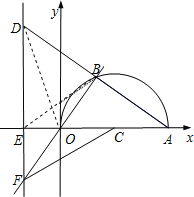
ЁпOAЪЧЁбCжБОЖЃЌ
ЁрЁЯOBA=90ЁуЃЌ
гжЁпAB=BDЃЌ
ЁрOBЪЧADЕФДЙжБЦНЗжЯпЃЌ
ЁрOD=OA=10ЃЌ
дкRtЁїODEжаЃЌ
OE=![]() =
=![]() ЃЌ
ЃЌ
ЁрAE=AO+OE=20+12=32ЃЌ
гЩЁЯAOB=ЁЯADE=90ЁуЁЯOABЃЌЁЯOEF=ЁЯDEAЃЌ
ЕУЁїOEFЁзЁїDEA
Ёр![]() ,МД
,МД![]() ЃЌ
ЃЌ
ЁрEF=24ЃЛ
ЁрEF=6Лђ24ЃЛ
(3)ЩшOE=xЃЌ
ЂйЕБНЛЕуEдкOЃЌCжЎМфЪБЃЌгЩвдЕуE. C.FЮЊЖЅЕуЕФШ§НЧ
аЮгыЁїAOBЯрЫЦЃЌгаЁЯECF=ЁЯBOAЛђЁЯECF=ЁЯOABЃЌ
ЕБЁЯECF=ЁЯBOAЪБЃЌДЫЪБЁїOCFЮЊЕШбќШ§НЧаЮЃЌЕуEЮЊOC
жаЕу,МДOE=5ЃЌ
ЁрE (5,0)ЃЛ
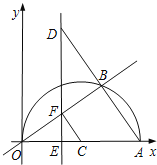
ЕБЁЯECF=ЁЯOABЪБЃЌгаCE=10xЃЌAE=20xЃЌ
ЁрCFЁЮAB,гаCF=![]() ABЃЌ
ABЃЌ
ЁпЁїECFЁзЁїEADЃЌ
Ёр![]() ,МД
,МД![]() ,НтЕУЃКx=
,НтЕУЃКx=![]() ЃЌ
ЃЌ
ЁрE (![]() ,0)ЃЛ
,0)ЃЛ
ЂкЕБНЛЕуEдкЕуCЕФгвВрЪБЃЌ
ЁпЁЯECF>ЁЯBOAЃЌ
ЁрвЊЪЙЁїECFгыЁїBAOЯрЫЦ,жЛФмЪЙЁЯECF=ЁЯBAO,
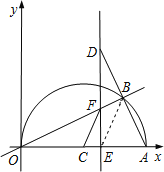
СЌНгBEЃЌ
ЁпBEЮЊRtЁїADEаББпЩЯЕФжаЯпЃЌ
ЁрBE=AB=BDЃЌ
ЁрЁЯBEA=ЁЯBAOЃЌ
ЁрЁЯBEA=ЁЯECFЃЌ
ЁрCFЁЮBEЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯECF=ЁЯBAO,ЁЯFEC=ЁЯDEA=90ЁуЃЌ
ЁрЁїCEFЁзЁїAEDЃЌ
ЁрCFAD=CEAEЃЌ
ЖјAD=2BEЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ,НтЕУx =
,НтЕУx =![]() ,x =
,x =![]() <0(ЩсШЅ)ЃЌ
<0(ЩсШЅ)ЃЌ
ЁрE (![]() ,0)ЃЛ
,0)ЃЛ
ЂлЕБНЛЕуEдкЕуOЕФзѓВрЪБЃЌ
ЁпЁЯBOA=ЁЯEOF>ЁЯECF.
ЁрвЊЪЙЁїECFгыЁїBAOЯрЫЦ,жЛФмЪЙЁЯECF=ЁЯBAO

СЌНгBE,ЕУBE=![]() AD=ABЃЌЁЯBEA=ЁЯBAO
AD=ABЃЌЁЯBEA=ЁЯBAO
ЁрЁЯECF=ЁЯBEAЃЌ
ЁрCFЁЮBEЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁпЁЯECF=ЁЯBAO,ЁЯFEC=ЁЯDEA=90ЃЌ
ЁрЁїCEFЁзЁїAEDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЖјAD=2BEЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУx=![]() ,x=
,x=![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ
ЁпЕуEдкxжсИКАыжсЩЯЃЌ
Ёр![]() (
(![]() ,0)ЃЌ
,0)ЃЌ
злЩЯЫљЪіЃКДцдквдЕуE. C.FЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЃЌ
ДЫЪБЕуEзјБъЮЊЃКEЕуЮЊ![]() .
.
ЕуОІ: НтД№БОЬтЕФЙиМќЪЧЪьСЗеЦЮеЯрЫЦШ§НЧаЮЕФаджЪЃКЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌзЂвтЖдгІзжФИдкЖдгІЮЛжУЩЯ.