题目内容
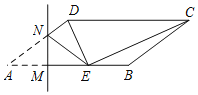
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度,沿
个单位长度的速度,沿![]() 边向终点
边向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,连结
,连结![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
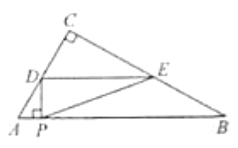
(1)当点![]() 在
在![]() 边上时,
边上时,![]() 的长为________(用含
的长为________(用含![]() 的代数式表示 )
的代数式表示 )
(2)当点![]() 为AC边的中点时,求
为AC边的中点时,求![]() 的值.
的值.
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当边![]() 与
与![]() 的边垂直时,直接写出
的边垂直时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当0<t<1时,
;(3)当0<t<1时,![]() ; 当1<t<4时,
; 当1<t<4时,![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)直接利用tan∠A进行计算即可;(2)先求出AC,进而求出AD,再利用直角三角形ADP求出AP即可;(3)分出情况,当D点在AC上与D点在BC上,利用相似三角形求出线段长,然后利用三角形面积进行解题即可(4)同样分出情况,当PE垂直AC或者PE垂直BC时的情况,然后利用三角形相似可直接解出t
(1)∠A=60°,tan∠A=tan60°=![]() =
=![]() ,得到DP=
,得到DP=![]()
(2)∠A=60°,AB=4,得到AC=2
当D为AC中点时,AD=1,在直角三角形ADP中,∠ADP=30°,所以AP=![]()
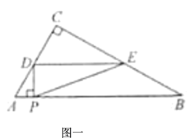
(3)当t=1时,D点与C点重合,
①当0<t<1时,如图一,由第一问得到DP=![]() ,DA=2t,AC=2,AB=4,DC=2-2t,
,DA=2t,AC=2,AB=4,DC=2-2t,
∵ED∥AB
∴△DCE∽△ACB
∴![]() 即
即![]()
∴DE=4-4t
∴S△PDE=![]() DE·DP 即
DE·DP 即![]()
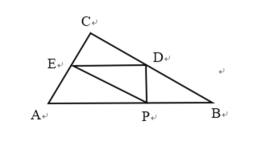
当1<t<4时,如图二BC=2![]() AP=t,BP=4-t,BD=
AP=t,BP=4-t,BD=![]() =
=![]() (4-t),CD=BC-BD=
(4-t),CD=BC-BD=![]() (t-1),因为ED∥AB,有△DCE∽△BCA,得到
(t-1),因为ED∥AB,有△DCE∽△BCA,得到![]() ,即
,即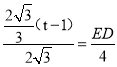 ,解出ED=
,解出ED=![]() (t-1)
(t-1)
S△PDE=![]() DE·DP 即
DE·DP 即![]()
(4)![]() 或
或![]() .
.

练习册系列答案
相关题目