ΧβΡΩΡΎ»ί
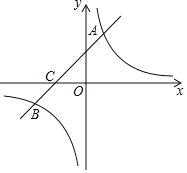
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy1ΘΫax2+bx+![]() ”κx÷αΫΜ”ΎΒψAΘ®©¹3Θ§0Θ©Θ§ΒψBΘ§ΒψD «≈ΉΈοœΏy1ΒΡΕΞΒψΘ§ΙΐΒψDΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣΒψCΘ®©¹1Θ§0Θ©Θ°
”κx÷αΫΜ”ΎΒψAΘ®©¹3Θ§0Θ©Θ§ΒψBΘ§ΒψD «≈ΉΈοœΏy1ΒΡΕΞΒψΘ§ΙΐΒψDΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣΒψCΘ®©¹1Θ§0Θ©Θ°
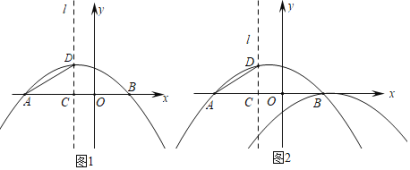
Θ®1Θ©«σ≈ΉΈοœΏy1ΥυΕ‘”ΠΒΡΚ· ΐΫβΈω ΫΘΜ
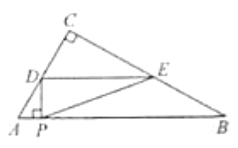
Θ®2Θ©»γΆΦ1Θ§ΒψM‘Ύ≈ΉΈοœΏy1…œΘ§ΚαΉχ±ξΈΣmΘ§Ν§Ϋ”MCΘ§»τΓœMCBΘΫΓœDACΘ§«σmΒΡ÷ΒΘΜ
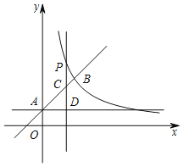
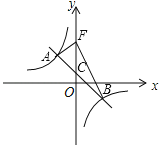
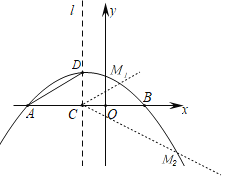
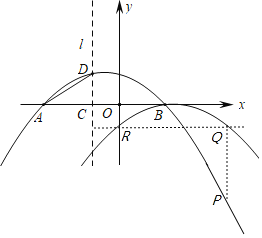
Θ®3Θ©»γΆΦ2Θ§ΫΪ≈ΉΈοœΏy1ΤΫ“ΤΚσΒΟΒΫΕΞΒψΈΣBΒΡ≈ΉΈοœΏy2Θ°ΒψPΈΣ≈ΉΈοœΏy1…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψPΉςy÷αΒΡΤΫ––œΏΘ§ΫΜ≈ΉΈοœΏy2”ΎΒψQΘ§ΙΐΒψQΉςx÷αΒΡΤΫ––œΏΘ§ΫΜ≈ΉΈοœΏy2”ΎΒψRΘ°Β±“‘ΒψPΘ§QΘ§RΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςACD»ΪΒ» ±Θ§«κ÷±Ϋ”–¥≥ωΒψPΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©mΒΡ÷ΒΈΣ
ΘΜΘ®2Θ©mΒΡ÷ΒΈΣ![]() Μρ©¹2+
Μρ©¹2+![]() ΘΜΘ®3Θ©PΒψΉχ±ξΈΣΘ®0Θ§
ΘΜΘ®3Θ©PΒψΉχ±ξΈΣΘ®0Θ§![]() Θ©ΜρPΘ®2Θ§©¹
Θ©ΜρPΘ®2Θ§©¹![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
(1)ΗυΨίAΓΔCΝΫΒψΒΡΉχ±ξ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ωΫβΈω ΫΘΜ
(2)»γΆΦΘ§Β±MΒψ‘Ύx÷α…œΖΫ ±Θ§»τΓœM1CBΘΫΓœDACΘ§‘ρDAΓΈCM1Θ§œ»«σ÷±œΏADΒΡΫβΈω ΫΘ§”…ΒψCΒΡΉχ±ξΩ…«σ≥ω÷±œΏCM1ΒΡΫβΈω ΫΘ§ΝΣΝΔ÷±œΏΚΆ≈ΉΈοœΏΖΫ≥ΧΩ…«σ≥ωΒψM1ΒΡΉχ±ξΘ§Β±ΒψM‘Ύx÷αœ¬ΖΫ ±Θ§”…÷αΕ‘≥ΤΒΡ–‘÷ Ω…«σ≥ω÷±œΏCM2ΒΡΫβΈω ΫΘ§Ά§άμΝΣΝΔ÷±œΏΚΆ≈ΉΈοœΏΖΫ≥Χ‘ρ«σ≥ωΒψMΒΡΉχ±ξΘΜ
(3)œ»«σ≥ωy2ΒΡΫβΈω ΫΘ§Ω……η≥ωΒψPΉχ±ξΘ§±μ ΨQΓΔRΉχ±ξΦΑPQΓΔQRΘ§ΗυΨί“‘PΘ§QΘ§RΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςACD»ΪΒ»Θ§Ζ÷άύΧ÷¬έΕ‘”Π±ΏœύΒ»ΒΡΩ…Ρή–‘Φ¥Ω…«σPΒψΉχ±ξΘ°
(1)”…Χβ“βΒΟΘΚ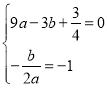 Θ§ΫβΒΟ
Θ§ΫβΒΟ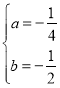 Θ§
Θ§
≈ΉΈοœΏy1ΥυΕ‘”ΠΒΡΚ· ΐΫβΈω ΫΈΣ![]() ΘΜ
ΘΜ
(2)Β±xΘΫ©¹1 ±Θ§yΘΫ![]() =1Θ§
=1Θ§
ΓύD(©¹1Θ§1)Θ§
…η÷±œΏADΒΡΫβΈω ΫΈΣyΘΫkx+nΘ§
Γύ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏADΒΡΫβΈω ΫΈΣyΘΫ![]() x+
x+![]() Θ§
Θ§
»γΆΦΘ§ΔΌΒ±MΒψ‘Ύx÷α…œΖΫ ±Θ§
ΓΏΓœM1CBΘΫΓœDACΘ§
ΓύDAΓΈCM1Θ§
…η÷±œΏCM1ΒΡΫβΈω ΫΈΣyΘΫ![]() x+b1Θ§
x+b1Θ§
ΓΏ÷±œΏΨ≠ΙΐΒψCΘ§
Γύ-![]() +b1=0Θ§ΫβΒΟΘΚb1=
+b1=0Θ§ΫβΒΟΘΚb1=![]() Θ§
Θ§
Γύ÷±œΏCM1ΒΡΫβΈω ΫΈΣyΘΫ![]() x+
x+![]() Θ§
Θ§
Γύ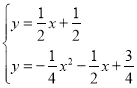 Θ§
Θ§
ΫβΒΟΘΚx=-2+![]() Θ§x=-2-
Θ§x=-2-![]() (…α»Ξ)Θ§
(…α»Ξ)Θ§
ΓύmΘΫ©¹2+![]() Θ§
Θ§
ΔΎΒ±ΒψM‘Ύx÷αœ¬ΖΫ ±Θ§÷±œΏCM2”κ÷±œΏCM1ΙΊ”Ύx÷αΕ‘≥ΤΘ§
”…÷αΕ‘≥ΤΒΡ–‘÷ Ω…ΒΟ÷±œΏCM2ΒΡΫβΈω ΫΈΣyΘΫ-![]() x-
x-![]() Θ§
Θ§
Γύ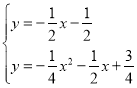 Θ§ΫβΒΟΘΚx=
Θ§ΫβΒΟΘΚx=![]() ΜρxΘΫ©¹
ΜρxΘΫ©¹![]() (…α»Ξ)Θ§
(…α»Ξ)Θ§
Γύm=![]() Θ§
Θ§
ΉέΚœ“‘…œΩ…ΒΟmΒΡ÷ΒΈΣ![]() Μρ©¹2+
Μρ©¹2+![]() ΘΜ
ΘΜ
(3)ΓΏ≈ΉΈοœΏy1ΤΫ“ΤΚσΒΟΒΫy2Θ§«“ΕΞΒψΈΣB(1Θ§0)Θ§
Γύ![]() Θ§
Θ§
Φ¥y2=![]() Θ§
Θ§
…ηP(mΘ§![]() )Θ§‘ρQ(mΘ§
)Θ§‘ρQ(mΘ§![]() )Θ§
)Θ§
ΓύR(2©¹mΘ§![]() )Θ§
)Θ§
ΔΌΒ±P‘ΎQΒψ…œΖΫ ±Θ§
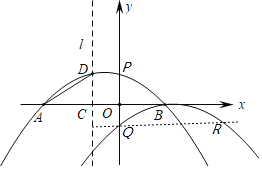
PQΘΫ1©¹mΘ§QRΘΫ2©¹2mΘ§
ΓΏΓςPQR”κΓςACD»ΪΒ»Θ§
ΓύΒ±PQΘΫDC«“QRΘΫAC ±Θ§mΘΫ0Θ§
ΓύP(0Θ§![]() )Θ§R(2Θ§©¹
)Θ§R(2Θ§©¹![]() )Θ§
)Θ§
Β±PQΘΫAC«“QRΘΫDC ±Θ§ΈόΫβΘΜ
ΔΎΒ±ΒψP‘ΎQΒψœ¬ΖΫ ±Θ§
Ά§άμΘΚPQΘΫm©¹1Θ§QRΘΫ2m©¹2Θ§
m©¹1ΘΫ1Θ§
ΓύmΘΫ2Θ§
‘ρP(2Θ§![]() )Θ§R(0Θ§©¹
)Θ§R(0Θ§©¹![]() )Θ§
)Θ§
ΉέΚœΩ…ΒΟPΒψΉχ±ξΈΣ(0Θ§![]() )ΜρP(2Θ§
)ΜρP(2Θ§![]() )Θ°
)Θ°

 ÷–ΩΦΫβΕΝΩΦΒψΨΪΝΖœΒΝ–¥πΑΗ
÷–ΩΦΫβΕΝΩΦΒψΨΪΝΖœΒΝ–¥πΑΗ