题目内容
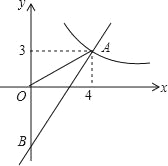
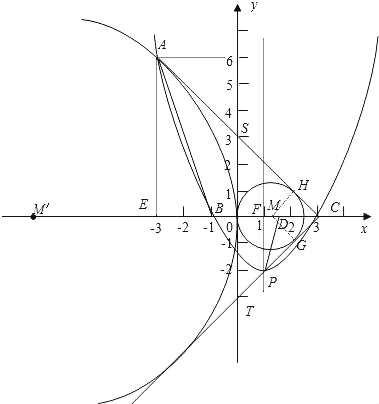
【题目】已知二次函数y=![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
(1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象;
(2)设D为线段OC上的一点,满足∠DPC=∠BAC,求点D的坐标;
(3)在x轴上是否存在一点M,使以M为圆心的圆与AC、PC所在的直线及y轴都相切?如果存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣x﹣
x2﹣x﹣![]() ; P(1,﹣2),C(3,0)(2)D(
; P(1,﹣2),C(3,0)(2)D(![]() ,0)(3)存在
,0)(3)存在
【解析】试题分析:(1)利用待定系数法求出![]() 的值后可求出该函数的解析式;
的值后可求出该函数的解析式;
(2)证明![]() 利用线段比求出各相关线段的值后易求点
利用线段比求出各相关线段的值后易求点![]() 的坐标;
的坐标;
(3)过M作MH⊥AC,MG⊥PC垂足分别为H、G,推出![]() 是等腰直角三角形,M是
是等腰直角三角形,M是![]() 的内切圆圆心,根据直线与圆的关系进行解答.
的内切圆圆心,根据直线与圆的关系进行解答.
试题解析:(1)∵二次函数![]() 的图象过点A(3,6),B(1,0),
的图象过点A(3,6),B(1,0),
得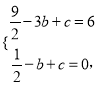
解得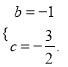
∴这个二次函数的解析式为:
![]()
由解析式可求P(1,2),C(3,0),
画出二次函数的图象;
(2)解法一:
易证: ![]()
又已知:∠DPC=∠BAC,
∴△DPC∽△BAC,
![]()
易求![]()
![]()
![]()
![]()
解法二:过A作AE⊥x轴,垂足为E,
设抛物线的对称轴交x轴于F,
亦可证△AEB∽△PFD,
![]()
易求:AE=6,EB=2,PF=2,
![]()
![]()
![]()
(3)存在.
①过M作MH⊥AC,MG⊥PC垂足分别为H、G,设AC交y轴于S,CP的延长线交y轴于T,
∵△SCT是等腰直角三角形,M是△SCT的内切圆圆心,
∴MG=MH=OM,
又![]() 且OM+MC=OC,
且OM+MC=OC,
![]() 得
得![]()
![]()
②在x轴的负半轴上,存在一点M′,
同理OM′+OC=M′C, ![]()
得![]()
![]()
即在x轴上存在满足条件的两个点.

 阅读快车系列答案
阅读快车系列答案【题目】(7分)某产品每件的成本10元,试销阶段每件产品的销售价![]() (元)与产品的日销售量
(元)与产品的日销售量![]() (件)之间的关系如下表:
(件)之间的关系如下表:
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
且日销售量![]() (件)是销售价
(件)是销售价![]() (元)的一次函数.
(元)的一次函数.
(1)求出日销售量![]() (件)与销售价
(件)与销售价![]() (元)的函数关系式;
(元)的函数关系式;
(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时最大销售利润是多少?