题目内容

若一个三角形的三个内角之比是2：4：6，那么这个三角形是

A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
不能构成三角形

B
分析：已知三角形三个内角的度数之比，可以设一份为k，根据三角形的内角和等于180°列方程求三个内角的度数，从而确定三角形的形状．
解答：∵三角形的三个内角之比是2：4：6，
∴设三角形的三个内角的度数分别为2k，4k，6k，
∴2k+4k+6k=180°，解得k=15°，
∴6k=90°，
∴这个三角形是直角三角形．
故选B．
点评：本题考查的是三角形内角和定理，熟知“三角形内角和是180°”是解答此题的关键．

练习册系列答案

新起点百分百单元测试卷系列答案

状元口算计算系列答案

题库精选系列答案

复习与测评单元综合测试卷系列答案

小学毕业总复习北京教育出版社系列答案

名校有约小学毕业升学总复习系列答案

初中毕业升学考试指南系列答案

组合阅读训练系列答案

名校名师测试卷系列答案

期末复习第1卷系列答案

相关题目

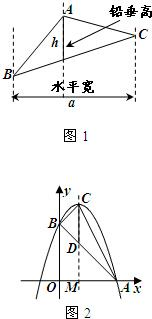阅读材料：如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”（h）．我们可得出一种计算三角形面积的新方法：S_△ABC=

ah，即三角形面积等于水平宽与铅垂高乘积的一半．
解答下列问题：
如图2，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），点P是抛物线（在第一象限内）上的一个动点．
（1）求抛物线的解析式；
（2）若点B为抛物线与y轴的交点，求直线AB的解析式；
（3）在（2）的条件下，设抛物线的对称轴分别交AB、x轴于点D、M，连接PA、PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S_△CAB；
（4）在（2）的条件下，设P点的横坐标为x，△PAB的铅垂高为h、面积为S，请分别写出h和S关于x的函数关系式．

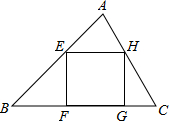某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨：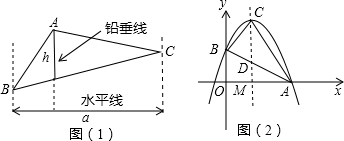
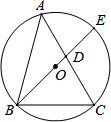定义：如果一个正方形的四个顶点都在一个三角形的边上，那么我们就把这个正方形叫做三角形的内接正方形．
结论：在探讨过程中，有三位同学得出如下结果：
甲同学：在钝角、直角、不等边锐角三角形中分别存在

个大小不同的内接正方形．
乙同学：在直角三角形中，两个顶点都在斜边上的内接正方形的面积较大．
丙同学：在不等边锐角三角形中，两个顶点都在较大边上的内接正方形的面积反而较小．
任务：（1）填充甲同学结论中的数据；
（2）乙同学的结果正确吗？若不正确，请举出一个反例并通过计算给予说明，若正确，请给出证明；
（3）请你结合（2）的判定，推测丙同学的结论是否正确，并证明．

阅读材料：
如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”（h）．我们可得出一种计算三角形面积的新方法：S△ABC=ah，即三角形面积等于水平宽与铅垂高乘积的一半．

解答下列问题：
如图2，抛物线顶点坐标为点C（1，4），交x轴于点A（3，0），点P是抛物线（在第一象限内）上的一个动点．
（1）求抛物线的解析式；
（2）若点B为抛物线与y轴的交点，求直线AB的解析式；
（3）设点P是抛物线（第一象限内）上的一个动点，是否存在一点P，使S_△PAB=S_△CAB？若存在，求出点P的坐标；若不存在，请说明理由．

学习了勾股定理的逆定理，我们知道：在一个三角形中，如果两边的平方和等于第三边的平方，那么这个三角形为直角三角形．类似地，我们定义：对于任意的三角形，设其三个角的度数分别为x°、y°和z°，若满足x²+y²=z²，则称这个三角形为勾股三角形．
（1）根据“勾股三角形”的定义，请你直接判断命题：“直角三角形是勾股三角形”是真命题还是假命题？
（2）已知某一勾股三角形的三个内角的度数从小到大依次为x°、y°和z°，且xy=2160，求x+y的值；
（3）如图，△ABC内接于⊙O，AB=

，BC=2，⊙O的直径BE交AC于点D．
①求证：△ABC是勾股三角形；
②求DE的长．

已知在直角坐标平面内有双曲线y=

，另有△ABC，其中点A、B、C的坐标分别是A（-2

，0），C（0，

）．
（1）如果将△ABC沿x轴翻折后得到对应的△A₁B₁C₁ （其中点A、B、C的对应点分别是点A₁、B₁、C₁），问：△A₁B₁C₁的三个顶点中，有无在双曲线y=

上的点？若有，写出这个点的坐标．
（2）如果将△ABC沿x轴正方向平移a个单位后，使△ABC的一个顶点落在双曲线y=

上，请直接写出a的值．
（3）如果△ABC关于原点O的对称的三角形△A₂B₂C₂（其中点A、B、C的对应点分别是点A₂、B₂、C₂），请写出经过点A、A₂的直线所表示的函数解析式．