��Ŀ����
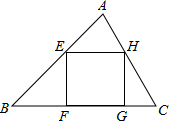 ij����ѧϰС����һ�λ�ж������ε��ڽ������ε��й����������̽�֣�
ij����ѧϰС����һ�λ�ж������ε��ڽ������ε��й����������̽�֣����壺���һ�������ε��ĸ����㶼��һ�������εı��ϣ���ô���ǾͰ���������ν��������ε��ڽ������Σ�
���ۣ���̽�ֹ����У�����λͬѧ�ó����½����
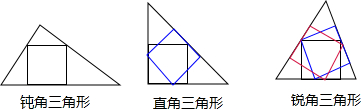
��ͬѧ���ڶ۽ǡ�ֱ�ǡ����ȱ�����������зֱ����
��ͬѧ����ֱ���������У��������㶼��б���ϵ��ڽ������ε�����ϴ�
��ͬѧ���ڲ��ȱ�����������У��������㶼�ڽϴ���ϵ��ڽ������ε����������С��
����1������ͬѧ�����е����ݣ�
��2����ͬѧ�Ľ����ȷ��������ȷ����ٳ�һ��������ͨ���������˵��������ȷ�������֤����
��3�������ϣ�2�����ж����Ʋ��ͬѧ�Ľ����Ƿ���ȷ����֤����
��������1���ֱ�һ�¼��ɵó��𰸣�
��2�����жϣ��پ�һ�����ӣ����磺��Rt��ABC�У���B=90�㣬AB=BC=1����AC=
��
��3�����жϣ��پ�һ�����ӣ����ABC�������߷ֱ�Ϊa��b��c��������a��b��c���������ϵĶ�Ӧ�߷ֱ�Ϊha��hb��hc���ڽ������εı߳��ֱ�Ϊxa��xb��xc��
��2�����жϣ��پ�һ�����ӣ����磺��Rt��ABC�У���B=90�㣬AB=BC=1����AC=
| 2 |
��3�����жϣ��پ�һ�����ӣ����ABC�������߷ֱ�Ϊa��b��c��������a��b��c���������ϵĶ�Ӧ�߷ֱ�Ϊha��hb��hc���ڽ������εı߳��ֱ�Ϊxa��xb��xc��
��� �⣺��1��1��2��3����3�֣�
�⣺��1��1��2��3����3�֣�
��2����ͬѧ�Ľ������ȷ����4�֣�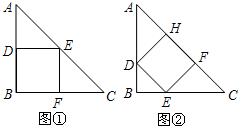
���磺��Rt��ABC�У���B=90�㣬AB=BC=1����AC=
��
��ͼ�٣��ı���DEFB��ֻ��һ��������б���ϵ��ڽ������Σ�
�����ı߳�Ϊa����������ɵã�
=
����a=
��
��ͼ�ڣ��ı���DEFH�������㶼��б���ϵ��ڽ������Σ�
�����ı߳�Ϊb����������ɵã�
=
����b=
��
��a��b����7�֣�
��3����ͬѧ�Ľ�����ȷ��
���ABC�������߷ֱ�Ϊa��b��c��������a��b��c���������ϵĶ�Ӧ�߷ֱ�Ϊha��hb��hc���ڽ������εı߳��ֱ�Ϊxa��xb��xc��
������ɵã�
=
����xa=
��ͬ��xb=
��
��xa-xb=
-
=
-
=2S��
-
��
=
��b+hb-a-ha����
=
��b+
-a-
����
=
•��b-a����1-
����
=
•��b-a����1-
����
�֡�b��a��ha��b���ࣨb-a����1-
����0��
��xa��xb����xa2��xb2��
���ڲ��ȱ�����������У��������㶼�ڽϴ���ϵ��ڽ������ε����������С����10�֣�
 �⣺��1��1��2��3����3�֣�
�⣺��1��1��2��3����3�֣���2����ͬѧ�Ľ������ȷ����4�֣�

���磺��Rt��ABC�У���B=90�㣬AB=BC=1����AC=
| 2 |
��ͼ�٣��ı���DEFB��ֻ��һ��������б���ϵ��ڽ������Σ�
�����ı߳�Ϊa����������ɵã�
| a |
| 1 |
| 1-a |
| 1 |
| 1 |
| 2 |
��ͼ�ڣ��ı���DEFH�������㶼��б���ϵ��ڽ������Σ�
�����ı߳�Ϊb����������ɵã�
| b | ||
|
| ||||
|
| ||
| 3 |
��a��b����7�֣�
��3����ͬѧ�Ľ�����ȷ��
���ABC�������߷ֱ�Ϊa��b��c��������a��b��c���������ϵĶ�Ӧ�߷ֱ�Ϊha��hb��hc���ڽ������εı߳��ֱ�Ϊxa��xb��xc��
������ɵã�
| xa |
| a |
| ha-xa |
| ha |
| aha |
| a+ha |
| bhb |
| b+hb |
��xa-xb=
| aha |
| a+ha |
| bhb |
| b+hb |
| 2S |
| a+ha |
| 2S |
| b+hb |
=2S��
| 1 |
| a+ha |
| 1 |
| b+ hb |
=
| 2S |
| (a+ha)(b+hb) |
=
| 2S |
| (a+ha)(b+hb) |
| 2S |
| b |
| 2S |
| a |
=
| 2S |
| (a+ha)(b+hb) |
| 2S |
| ab |
=
| 2S |
| (a+ha)(b+hb) |
| ha |
| b |
�֡�b��a��ha��b���ࣨb-a����1-
| ha |
| b |
��xa��xb����xa2��xb2��
���ڲ��ȱ�����������У��������㶼�ڽϴ���ϵ��ڽ������ε����������С����10�֣�
������������һ���ѶȽϴ����Ŀ�����������������ε��ж��������Լ������ε����ʣ��ٳ������ǽ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ

 ������
������ ���������ϵĶ�Ӧ�߷ֱ�Ϊ
���������ϵĶ�Ӧ�߷ֱ�Ϊ ���ڽ������εı߳��ֱ�Ϊ
���ڽ������εı߳��ֱ�Ϊ .����Ա�С��֤�������ѣ���ֱ���á�
.����Ա�С��֤�������ѣ���ֱ���á� ��������ۣ�����֤����ȷ������¿�1�֣�.
��������ۣ�����֤����ȷ������¿�1�֣�.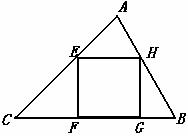
 ������
������ ���������ϵĶ�Ӧ�߷ֱ�Ϊ
���������ϵĶ�Ӧ�߷ֱ�Ϊ ���ڽ������εı߳��ֱ�Ϊ
���ڽ������εı߳��ֱ�Ϊ .����Ա�С��֤�������ѣ���ֱ���á�
.����Ա�С��֤�������ѣ���ֱ���á� ��������ۣ�����֤����ȷ������¿�1�֣�.
��������ۣ�����֤����ȷ������¿�1�֣�.