题目内容
 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.(1)根据“勾股三角形”的定义,请你直接判断命题:“直角三角形是勾股三角形”是真命题还是假命题?
(2)已知某一勾股三角形的三个内角的度数从小到大依次为x°、y°和z°,且xy=2160,求x+y的值;
(3)如图,△ABC内接于⊙O,AB=
| 6 |
| 3 |
①求证:△ABC是勾股三角形;
②求DE的长.
分析:(1)直接根据“勾股三角形”的定义,判断得出即可;
(2)利用已知得出等量量关系组成方程组,进而求出x+y的值;
(3)①过B作BH⊥AC于H,设AH=x,利用勾股定理首先得出AH=BH=
,HC=1,进而得出∠A=45°,∠C=60°,∠B=75°,即可得出答案;
②过D作DK⊥AB于K,设KD=h,首先得出h+
h=
,进而得出h的值,求出BD,进而得出DE的长.
(2)利用已知得出等量量关系组成方程组,进而求出x+y的值;
(3)①过B作BH⊥AC于H,设AH=x,利用勾股定理首先得出AH=BH=
| 3 |
②过D作DK⊥AB于K,设KD=h,首先得出h+
| 3 |
| 6 |
解答:解:(1)∵对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形,
∴无法得到,所有直角三角形是勾股三角形,故是假命题;
(2)由题意可得:
,
解得:x+y=102;
(3)①证明:过B作BH⊥AC于H,设AH=x,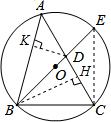
Rt△ABH中,BH=
,
Rt△CBH中,(
)2+(1+
-x)2=4,
解得:x=
,
所以,AH=BH=
,HC=1,
∴∠A=∠ABH=45°,
∴tan∠HBC=
=
=
,
∴∠HBC=30°,
∴∠BCH=60°,∠B=75°,
∴452+602=752
∴△ABC是勾股三角形;
②连接CE,
∵∠A=45°,
∴∠BEC=∠BAC=45°,
又∵BE是直径,
∴∠BCE=90°,
∴BC=CE=2,
过D作DK⊥AB于K,设KD=h,
∵∠EBC=45°,∠ABC=75°,
∴∠ABE=30°,
∴BK=
h,AK=h,
∴h+
h=
,
解得:h=
,
∴BD=2KD=2h=3
-
,
∴BE-BD=2
-(3
-
)=
-
.
∴无法得到,所有直角三角形是勾股三角形,故是假命题;
(2)由题意可得:
|
解得:x+y=102;
(3)①证明:过B作BH⊥AC于H,设AH=x,

Rt△ABH中,BH=
| 6-x2 |
Rt△CBH中,(
| 6-x2 |
| 3 |
解得:x=
| 3 |
所以,AH=BH=
| 3 |
∴∠A=∠ABH=45°,
∴tan∠HBC=
| CH |
| BH |
| 1 | ||
|
| ||
| 3 |
∴∠HBC=30°,
∴∠BCH=60°,∠B=75°,
∴452+602=752
∴△ABC是勾股三角形;
②连接CE,
∵∠A=45°,
∴∠BEC=∠BAC=45°,
又∵BE是直径,
∴∠BCE=90°,
∴BC=CE=2,
过D作DK⊥AB于K,设KD=h,
∵∠EBC=45°,∠ABC=75°,
∴∠ABE=30°,
∴BK=
| 3 |
∴h+
| 3 |
| 6 |
解得:h=
3
| ||||
| 2 |
∴BD=2KD=2h=3
| 2 |
| 6 |
∴BE-BD=2
| 2 |
| 2 |
| 6 |
| 6 |
| 2 |
点评:此题主要考查了新定义以及多元方程组解法以及勾股定理和锐角三角函数关系,利用勾股定理得出AH,HC的长是解题关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 下操作:
下操作: