��Ŀ����
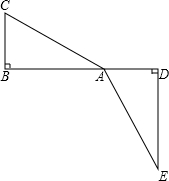
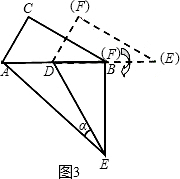
����ȫ�ȵ�Rt��ABC��Rt��EDA��ͼ���ã���B��A��D��ͬһ��ֱ���ϣ���������ͼ�У�����ABC��ƽ����BF������D��DF��BF������ΪF������CE��֤��BF��CE��
̽�����߶�BF��CE�Ĺ�ϵ����֤����Ľ��ۣ�
˵�����������֤��̽�����õĽ��ۣ����Խ�������ȫ�ȵ�Rt��ABC��Rt��EDA����Ϊ������ȫ�ȵĵ���ֱ�ǡ�ABC�͵���ֱ�ǡ�EDA����C��A��E��ͬһ��ֱ���ϣ����������������䣬������֤������֤����������2�֣�
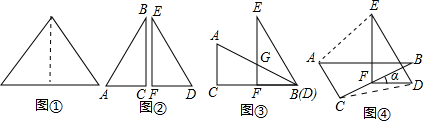
����������E��EG��CB���ӳ����ڵ�G���ɵá�BFD�͡�CGE�ǵ���ֱ�������Σ��ɵ�BF=
��AB+AD����CE=
��AB+AD�����ɴ˿ɵã�2BF=CE��
| ||
| 2 |
| 2 |
��� ֤����2BF=CE����BF��CE��
֤����2BF=CE����BF��CE��
����E��EG��CB���ӳ����ڵ�G���ɵ�BDEG�Ǿ��Σ���BD=EG��BG=DE��
��BC=AD=m��AB=DE=n��
��BF�ǡ�ABC��ƽ���ߣ�
���DBF=45�㣬
�֡�DF��BF��
���FDB=45�㣬
���BFD�ǵ���ֱ�������Σ�
��BF2+DF2=BD2��BF2+BF2=��AB+AD��2=��m+n��2��
��BF=
��m+n����
�֡ߡ�CGEҲ��ֱ�������Σ�
��CE2=CG2+GE2
=��CB+BG��2+BD2
=��CB+DE��2+��AB+AD��2
=��m+n��2+��m+n��2
=2��m+n��2
��CE=
��m+n����
�ɴ˿ɵã�2BF=CE��
�ߡ�GCE=��CBF=45�㣬
��CE��BF��
 ֤����2BF=CE����BF��CE��
֤����2BF=CE����BF��CE������E��EG��CB���ӳ����ڵ�G���ɵ�BDEG�Ǿ��Σ���BD=EG��BG=DE��
��BC=AD=m��AB=DE=n��
��BF�ǡ�ABC��ƽ���ߣ�
���DBF=45�㣬
�֡�DF��BF��
���FDB=45�㣬
���BFD�ǵ���ֱ�������Σ�
��BF2+DF2=BD2��BF2+BF2=��AB+AD��2=��m+n��2��
��BF=
| ||
| 2 |
�֡ߡ�CGEҲ��ֱ�������Σ�
��CE2=CG2+GE2
=��CB+BG��2+BD2
=��CB+DE��2+��AB+AD��2
=��m+n��2+��m+n��2
=2��m+n��2
��CE=
| 2 |
�ɴ˿ɵã�2BF=CE��
�ߡ�GCE=��CBF=45�㣬
��CE��BF��
���������⿼���˽�ƽ���ߵĶ����ֱ�������ε����ʣ����������ǹؼ�������Ƚ��ѣ�

��ϰ��ϵ�д�
�����Ŀ
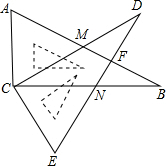 ��ͼ������ȫ�ȵ�Rt��ABC��Rt��EDC��ֱ�Ƕ��������һ�𣬡�B=��D=30�㣬AB��CD���ڵ�M��ED��BC���ڵ�N��AB��ED���ڵ�F��
��ͼ������ȫ�ȵ�Rt��ABC��Rt��EDC��ֱ�Ƕ��������һ�𣬡�B=��D=30�㣬AB��CD���ڵ�M��ED��BC���ڵ�N��AB��ED���ڵ�F��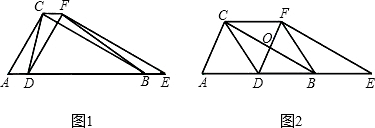
 ��2013•ʯ��ɽ��һģ����ͼ��������ȫ�ȵ�Rt��AOB��Rt��ECD�ֱ�����ƽ��ֱ������ϵxOy�У�ʹ��E���B�غϣ�ֱ�DZ�OB��BC��y���ϣ���֪��D ��4��2������A��D�����ֱ�߽�y���ڵ�F������ECD��DA������ÿ��
��2013•ʯ��ɽ��һģ����ͼ��������ȫ�ȵ�Rt��AOB��Rt��ECD�ֱ�����ƽ��ֱ������ϵxOy�У�ʹ��E���B�غϣ�ֱ�DZ�OB��BC��y���ϣ���֪��D ��4��2������A��D�����ֱ�߽�y���ڵ�F������ECD��DA������ÿ��