��Ŀ����
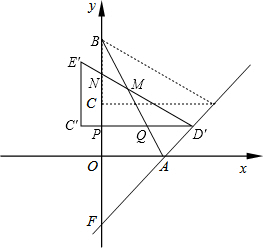
 ��2013•ʯ��ɽ��һģ����ͼ��������ȫ�ȵ�Rt��AOB��Rt��ECD�ֱ�����ƽ��ֱ������ϵxOy�У�ʹ��E���B�غϣ�ֱ�DZ�OB��BC��y���ϣ���֪��D ��4��2������A��D�����ֱ�߽�y���ڵ�F������ECD��DA������ÿ��
��2013•ʯ��ɽ��һģ����ͼ��������ȫ�ȵ�Rt��AOB��Rt��ECD�ֱ�����ƽ��ֱ������ϵxOy�У�ʹ��E���B�غϣ�ֱ�DZ�OB��BC��y���ϣ���֪��D ��4��2������A��D�����ֱ�߽�y���ڵ�F������ECD��DA������ÿ��| 2 |
��1����ֱ��AD�ĺ�������ʽ��
��2����̽���ڡ�ECDƽ�ƹ����У��ı���MNPQ������Ƿ�������ֵ�������ڣ����������ֵ��t��ȡֵ���������ڣ���˵�����ɣ�
��3����MNΪ�ߣ���E��D����·���������MNRH����������MNRH��������������������ʱt��ȡֵ��Χ��
��������1�����A��D��������꣬��ý���ʽ���ɣ�
��2�����ֱ��AB��BD��E��D��Ľ���ʽ������ƽ�Ƶ����ʣ��ɡ�MQD��ס�BJD���ó�S��MQD������ʾ���ı���MNPQ����������ö��κ���������ֵ��
��3�����������MNRH��������������������ʱ��H��x����ʱ����M��t��4-2t��������������������Ľ⣮
��2�����ֱ��AB��BD��E��D��Ľ���ʽ������ƽ�Ƶ����ʣ��ɡ�MQD��ס�BJD���ó�S��MQD������ʾ���ı���MNPQ����������ö��κ���������ֵ��
��3�����������MNRH��������������������ʱ��H��x����ʱ����M��t��4-2t��������������������Ľ⣮
����⣺��1��������A��2.0����
��D��4��2����
�ɵ�ֱ��AD����ʽ��y=x-2��
��2���ڡ�ECDƽ�ƹ����У��ı���MNPQ������������ֵ��
�������£�
��B��0��4����
�ɵ�ֱ��AB����ʽ��y=-2x+4��
ֱ��BD����ʽ��y=-
x+4��J��1��2����
�ڡ�ECDƽ��t��ʱ���ɡ�CDF=45�㣬
�ɵ�D�䣨4-t��2-t����N��0��4-
t����
��ֱ��E��D�����ʽΪ��y=-
x+4-
t��
�ɵ�M��t��4-2t����
Q��
��2-t����P��0��2-t��
�ɡ�MQD��ס�BJD����
=(
)2��
�ɵ�S��MQD��=3(1-
t)2��
S����E��C��PN=
t(2+2-
t)=-
t2+2t��
S�ı���MNPQ=S��E��C��D��- S��MQD��- S����E��C��PN
�൱t=1ʱ��S���=
��
��3������H��x����ʱ����M��t��4-2t������������ȣ�
��t=4-2t��
��t=
��
��0��t��
��
��D��4��2����
�ɵ�ֱ��AD����ʽ��y=x-2��
��2���ڡ�ECDƽ�ƹ����У��ı���MNPQ������������ֵ��

�������£�
��B��0��4����
�ɵ�ֱ��AB����ʽ��y=-2x+4��
ֱ��BD����ʽ��y=-
| 1 |
| 2 |
�ڡ�ECDƽ��t��ʱ���ɡ�CDF=45�㣬
�ɵ�D�䣨4-t��2-t����N��0��4-
| 3 |
| 2 |
��ֱ��E��D�����ʽΪ��y=-
| 1 |
| 2 |
| 3 |
| 2 |
�ɵ�M��t��4-2t����
Q��
| t+2 |
| 2 |
�ɡ�MQD��ס�BJD����
| S��MQD�� |
| S��BJD |
3-
| ||
| 3 |
�ɵ�S��MQD��=3(1-
| 1 |
| 2 |
S����E��C��PN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S�ı���MNPQ=S��E��C��D��- S��MQD��- S����E��C��PN
|
�൱t=1ʱ��S���=
| 3 |
| 2 |
��3������H��x����ʱ����M��t��4-2t������������ȣ�
��t=4-2t��
��t=
| 4 |
| 3 |
��0��t��
| 4 |
| 3 |
�����������ۺϿ���ƽ�Ƶ����ʣ����������Ƶ����ʣ����κ��������ʵ�֪ʶ�㣬�ѶȽϴ�

��ϰ��ϵ�д�
 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
�����Ŀ
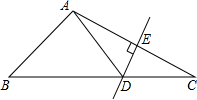 ��2013•ʯ��ɽ����ģ����ͼ����ABC�У�DE��AC�Ĵ�ֱƽ���ߣ�AE=4cm����ABD���ܳ�Ϊ14cm�����ABC���ܳ�Ϊ��������
��2013•ʯ��ɽ����ģ����ͼ����ABC�У�DE��AC�Ĵ�ֱƽ���ߣ�AE=4cm����ABD���ܳ�Ϊ14cm�����ABC���ܳ�Ϊ�������� ��2013•ʯ��ɽ����ģ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O�ϵ�һ�㣬��AC=8��AB=10��OD��BC�ڵ�D����BD�ij�Ϊ��������
��2013•ʯ��ɽ����ģ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O�ϵ�һ�㣬��AC=8��AB=10��OD��BC�ڵ�D����BD�ij�Ϊ��������