题目内容
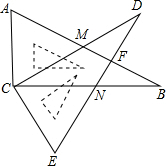 如图,两个全等的Rt△ABC、Rt△EDC的直角顶点放置在一起,∠B=∠D=30°,AB与CD交于点M,ED与BC交于点N,AB与ED交于点F.
如图,两个全等的Rt△ABC、Rt△EDC的直角顶点放置在一起,∠B=∠D=30°,AB与CD交于点M,ED与BC交于点N,AB与ED交于点F.(1)求证:△ACM≌△ECN;
(2)当∠MCN=30°时,找出MD与MF的数量关系,并加以说明.
分析:(1)欲证△ACM≌△ECN,可先由Rt△ABC、Rt△EDC全等的关系得出∠A=∠E,AC=CE又由∠ACM=∠ECN=90°-∠MCN可得出∠ACM=∠ECN即可由ASA得证;
(2)可由各角之间的数量关系先求出∠MFD=90°,再由∠D=30°可得出MD=2MF的数量关系;
(2)可由各角之间的数量关系先求出∠MFD=90°,再由∠D=30°可得出MD=2MF的数量关系;
解答:(1)证明:∵∠B=∠D,
∴∠A=∠E,
又∵AC=EC,
∠ACM=∠ECN=90°-∠MCN
在△ACM和△ECN中
,
∴△ACM≌△ECN(ASA);
(2)解:在Rt△ABC中,
∵∠B=30°,∠MCN=30°,
∴∠DMF=∠MCN+∠B=30°+30°=60°.
∵∠D=30°,
∴∠DFM=90°.
∴△MDF是直角三角形且∠D=30°.
∴MD=2MF.
∴∠A=∠E,
又∵AC=EC,
∠ACM=∠ECN=90°-∠MCN
在△ACM和△ECN中
|
∴△ACM≌△ECN(ASA);
(2)解:在Rt△ABC中,
∵∠B=30°,∠MCN=30°,
∴∠DMF=∠MCN+∠B=30°+30°=60°.
∵∠D=30°,
∴∠DFM=90°.
∴△MDF是直角三角形且∠D=30°.
∴MD=2MF.
点评:三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法去判定.

练习册系列答案
相关题目
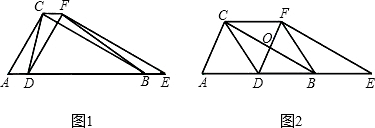
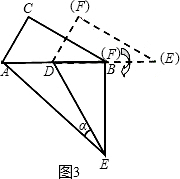
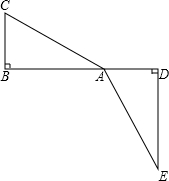
 (2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒
(2013•石景山区一模)如图,把两个全等的Rt△AOB和Rt△ECD分别置于平面直角坐标系xOy中,使点E与点B重合,直角边OB、BC在y轴上.已知点D (4,2),过A、D两点的直线交y轴于点F.若△ECD沿DA方向以每秒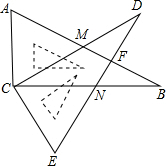 如图,两个全等的Rt△ABC、Rt△EDC的直角顶点放置在一起,∠B=∠D=30°,AB与CD交于点M,ED与BC交于点N,AB与ED交于点F.
如图,两个全等的Rt△ABC、Rt△EDC的直角顶点放置在一起,∠B=∠D=30°,AB与CD交于点M,ED与BC交于点N,AB与ED交于点F.