题目内容
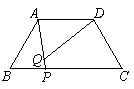
如图，等腰梯形ABCD中，AB = CD，AD//BC，AD = 2，BC = 4，
．
如果P是BC上一点，Q是AP上一点，且
．
⑴求证：⊿ABP ∽⊿DQA；
⑵当点P在BC上移动时，线段DQ的长度也随之变化，设PA = x，DQ = y，求y与x之间的函数关系式，并指出x的取值范围．
(1) ∵，，∴
，
∵AD//BC，∴
，又，
∴⊿ABP ∽⊿DQA．
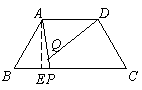
(2) 过点A作
，E是垂足．
在等腰梯形ABCD中，AB = CD，AD//BC，AD = 2，BC = 4，
∴
，
在
中，
，，
∴
，
∵⊿ABP ∽⊿DQA，∴
，
又∵PA = x，DQ = y，∴
，
∴
，
．
练习册系列答案
相关题目
14、如图，等腰梯形ABCD中，AB∥CD，∠A=60°，BD平分∠ABC，若梯形ABCD的周长为40cm，则CD的长为（ ）
24、已知：如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC．
（2007•昌平区二模）已知：如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC，∠A=120°，BD=
如图，等腰梯形ABCD中，AD∥BC，AB=CD，对角线BD平分∠ABC，且BD⊥DC，上底AD=3cm．
如图，等腰梯形ABCD中，AD∥BC，AB=CD，BD平分∠ABC，BD⊥DC，延长BC到E，使CE=AD．