题目内容
在同一平面直角坐标系内直线y=x-1、双曲线 、抛物线y=-2x2+12x-15共有多少个交点
、抛物线y=-2x2+12x-15共有多少个交点
- A.5个
- B.6个
- C.7个
- D.8个
A
分析:对于一次函数y=x-1和反比例函数线 ,一次函数y=x-1和抛物线y=-2x2+12x-15共可分别联立它们的解析式解方程组,求交点个数;反比例函数和抛物线y=-2x2+12x-15可借助于它们的图象求交点个数.
,一次函数y=x-1和抛物线y=-2x2+12x-15共可分别联立它们的解析式解方程组,求交点个数;反比例函数和抛物线y=-2x2+12x-15可借助于它们的图象求交点个数.
解答:∵直线y=x-1,抛物线y=-2x2+12x-15,
∴x-1=-2x2+12x-15.
∴2x2-11x+14=0,
a=2,b=-11,c=14,
∴△=b2-4ac=121-4×2×14>0,
∴x=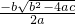 ,
,
∴x1= ,x2=2.
,x2=2.
∴交点坐标为( ,
, ),(2,1).
),(2,1).
∴直线y=x-1和抛物线y=-2x2+12x-15有两个交点.
∵直线y=x-1,双曲线 ,
,
∴x-1= ,
,
∴x2-x-2=0,
a=1,b=-1,c=-2,
∴△=b2-4ac=1-(-8)=9>0
∴x=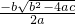 ,
,
∴x1=2,x2=-1.
∴交点坐标为(2,1),(-1,-2).
∴直线y=x-1和双曲线 有两个交点.
有两个交点.
把抛物线y=-2x2+12x-15配方的:y=-2(x-3)2+3,
∴顶点的坐标为(3,3).
当x=3时,双曲线 ,y=
,y= ,当x=3时,抛物线y=-2x2+12x-15=3,
,当x=3时,抛物线y=-2x2+12x-15=3,
∵ <3,
<3,
∴双曲线 和抛物线y=-2x2+12x-15,有两个交点.
和抛物线y=-2x2+12x-15,有两个交点.
∵当x=2时,抛物线y=1,
∴点(2,1)在抛物线y=-2x2+12x-15图象上.
在同一平面直角坐标系内直线y=x-1、双曲线 、抛物线y=-2x2+12x-15共有5个交点.
、抛物线y=-2x2+12x-15共有5个交点.
故选A.
点评:本题考查一次函数,反比例函数,二次函数的交点个数,解决此类问题的思路联立解析式解方程组即可.有时也要借助与它们的图象.
分析:对于一次函数y=x-1和反比例函数线
 ,一次函数y=x-1和抛物线y=-2x2+12x-15共可分别联立它们的解析式解方程组,求交点个数;反比例函数和抛物线y=-2x2+12x-15可借助于它们的图象求交点个数.
,一次函数y=x-1和抛物线y=-2x2+12x-15共可分别联立它们的解析式解方程组,求交点个数;反比例函数和抛物线y=-2x2+12x-15可借助于它们的图象求交点个数.解答:∵直线y=x-1,抛物线y=-2x2+12x-15,
∴x-1=-2x2+12x-15.
∴2x2-11x+14=0,
a=2,b=-11,c=14,
∴△=b2-4ac=121-4×2×14>0,
∴x=
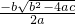 ,
,∴x1=
 ,x2=2.
,x2=2.∴交点坐标为(
 ,
, ),(2,1).
),(2,1).∴直线y=x-1和抛物线y=-2x2+12x-15有两个交点.
∵直线y=x-1,双曲线
 ,
,∴x-1=
 ,
,∴x2-x-2=0,
a=1,b=-1,c=-2,
∴△=b2-4ac=1-(-8)=9>0
∴x=
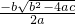 ,
,∴x1=2,x2=-1.
∴交点坐标为(2,1),(-1,-2).
∴直线y=x-1和双曲线
 有两个交点.
有两个交点.把抛物线y=-2x2+12x-15配方的:y=-2(x-3)2+3,
∴顶点的坐标为(3,3).
当x=3时,双曲线
 ,y=
,y= ,当x=3时,抛物线y=-2x2+12x-15=3,
,当x=3时,抛物线y=-2x2+12x-15=3,∵
 <3,
<3,∴双曲线
 和抛物线y=-2x2+12x-15,有两个交点.
和抛物线y=-2x2+12x-15,有两个交点.∵当x=2时,抛物线y=1,
∴点(2,1)在抛物线y=-2x2+12x-15图象上.
在同一平面直角坐标系内直线y=x-1、双曲线
 、抛物线y=-2x2+12x-15共有5个交点.
、抛物线y=-2x2+12x-15共有5个交点.故选A.
点评:本题考查一次函数,反比例函数,二次函数的交点个数,解决此类问题的思路联立解析式解方程组即可.有时也要借助与它们的图象.

练习册系列答案
相关题目


 直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )
直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )