题目内容
二元一次方程x-2y=0的解有无数个,其中它有一个解为
|
(1)请在下图中的平面直角坐标系中再描出三个以方程x-2y=0的解为坐标的点;
(2)过这四个点中的任意两点作直线,你有什么发现?直接写出结果;
(3)以方程x-2y=0的解为坐标的点的全体叫做方程x-2y=0的图象.想一想,方程x-2y=0的图象是什么?(直接回答)
(4)由(3)的结论,在同一平面直角坐标系中,画出二元一次方程组
|
分析:(1)先解出方程x-2y=0的三个解,再在平面直角坐标系中利用描点法解答;
(2)根据(1)的图象作答;
(3)由方程x-2y=0变形为y=
,即正比例函数,根据正比例函数图象的性质回答;
(4)在平面直角坐标系中分别画出x+y=1、2x-y=2的图象,两个图象的交点即为所求.
(2)根据(1)的图象作答;
(3)由方程x-2y=0变形为y=
| x |
| 2 |
(4)在平面直角坐标系中分别画出x+y=1、2x-y=2的图象,两个图象的交点即为所求.
解答:解:(1)二元一次方程x-2y=0的解可以为:
、
、
、
,
所以,以方程x-2y=0的解为坐标的点分别为:(2,1)、(4,2)、(1,
)、(3,
),
它们在平面直角坐标系中的图象如下图所示:
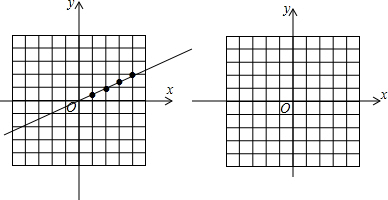
(2)由(1)图,知,四个点在一条直线上;
(3)由原方程,得y=
,
∵以方程x-2y=0的解为坐标的点的全体叫做方程x-2y=0的图象,
∴方程x-2y=0的图象就是正比例函数y=
的图象,
∵正比例函数y=
的图象是经过第一、三象限且过原点的一条直线,
∴方程x-2y=0的图象是经过第一、三象限且过原点的一条直线;
(4)①对于方程x+y=1,
当x=0时,y=1;
当y=0时,x=1;
所以方程x+y=1经过(0,1),(1,0)这两点;
②对于方程2x-y=2,
当x=0时,y=-2;
当y=0时,x=1;
所以方程x+y=1经过(0,-2),(1,0)这两点;
综合①②,在平面直角坐标系中画出的二元一次方程组
的图象如下所示: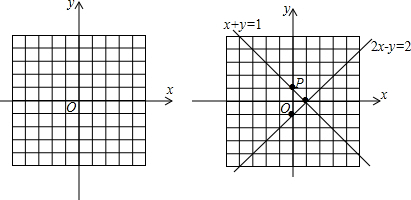
故原方程组的解是
,并且能在坐标系中用P(1,0)表示.
|
|
|
|
所以,以方程x-2y=0的解为坐标的点分别为:(2,1)、(4,2)、(1,
| 1 |
| 2 |
| 3 |
| 2 |
它们在平面直角坐标系中的图象如下图所示:

(2)由(1)图,知,四个点在一条直线上;
(3)由原方程,得y=
| x |
| 2 |
∵以方程x-2y=0的解为坐标的点的全体叫做方程x-2y=0的图象,
∴方程x-2y=0的图象就是正比例函数y=
| x |
| 2 |
∵正比例函数y=
| x |
| 2 |
∴方程x-2y=0的图象是经过第一、三象限且过原点的一条直线;
(4)①对于方程x+y=1,
当x=0时,y=1;
当y=0时,x=1;
所以方程x+y=1经过(0,1),(1,0)这两点;
②对于方程2x-y=2,
当x=0时,y=-2;
当y=0时,x=1;
所以方程x+y=1经过(0,-2),(1,0)这两点;
综合①②,在平面直角坐标系中画出的二元一次方程组
|

故原方程组的解是
|
点评:本题主要考查的是二元一次方程组的解及其直线方程的图象,题目比较长,要注意耐心解答.

练习册系列答案
相关题目