题目内容
已知:抛物线y=-x2+2mx-4m-m2(m是常数)与x轴有两个交点.
(1)当m取最大整数时,求出此抛物线的解析式;
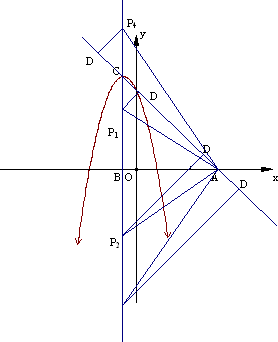
(2)设(1)中所求抛物线顶点为C,抛物线的对称轴与x轴交于点B,直线y=-x+3与x轴交于点A.点P为抛物线对称轴上一动点,过点P作PD⊥AC,垂足D在直线AC上.
若S△PAD=![]() S△ABC,求出点P的坐标.
S△ABC,求出点P的坐标.
答案:
解析:
解析:
|
(1)解:∵抛物线与x轴交于两点, ∴ 解得:m<0. 1分 ∴m<0时,抛物线与x轴有两个交点. 当m取最大的整数时, ∴m=-1. 即y=-x2-2x+3. 3分 (2)抛物线顶点C(-1,4),对称轴与x轴的交点B(-1,0).
直线y=-x+3与x轴交于点A,A(3,0) BA=BC,∠PCD=45°. ①当点D在线段AC上时,设PD=DC=x, AC= 根据题意,得 解得:x= 当x= P(-1,-2 当x=2 P(-1,2 ②当点D在AC的延长线上时,设PD=DC=x, 根据题意,得 解得:x= 当x=-2 当x=-2 P(-1,2 ③当点D在CA的延长线上时,设PD=DC=x, 根据题意,得 解得:x=2 当x=2 当x=2 P(-1,-2 P(-1,-2 |

练习册系列答案
相关题目
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左). ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).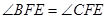 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由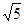 个单位长度、每秒2
个单位长度、每秒2
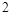 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).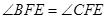 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2