题目内容
已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=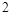 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).
1.求抛物线的解析式
2.设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得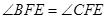 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由
3.射线OC上有两个动点P、Q同时从原点出发,分别以每秒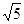 个单位长度、每秒2
个单位长度、每秒2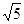 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
【答案】
1.点A(0,2m-7)代入y=-x2+2x+m-2,得m=5
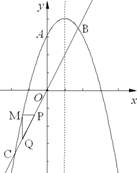
∴抛物线的解析式为y=-x2+2x+3
2.由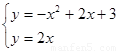 得
得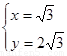 ,
,
∴B(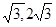 ),C(
),C(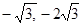 )
)
B(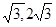 )关于抛物线对称轴
)关于抛物线对称轴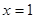 的
的
对称点为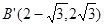
可得直线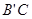 的解析式为
的解析式为 ,
,
由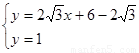 ,可得
,可得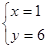
∴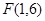 ………………………5分
………………………5分
3.当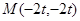 在抛物线上时,可得
在抛物线上时,可得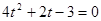 ,
,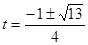 ,
,
当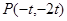 在抛物线上时,可得
在抛物线上时,可得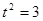 ,
,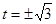 ,
,
舍去负值,所以t的取值范围是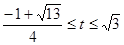 .………………8分
.………………8分
【解析】(1)将A点坐标代入解得抛物线的解析式;
(2)先求出抛物线与直线的交点B、C的坐标,然后求出B点关于抛物线对称轴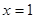 的对称点B′,从而得出B′C的解析式,再求出F点坐标;
的对称点B′,从而得出B′C的解析式,再求出F点坐标;
(3)把M、P两点的坐标代入抛物线方程中得出t的取值范围。

练习册系列答案
相关题目
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左). ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).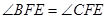 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由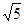 个单位长度、每秒2
个单位长度、每秒2