题目内容
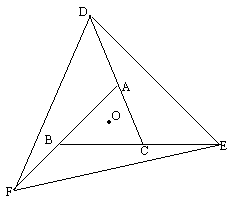
如图所示,已知△ABC的三个外角都是![]() ,D、E、F分别是CA、BC、AB延长线上的点,且AD=AC,CE=CB,AB=BF,连结DE、EF、FD,试问△DEF是什么三角形?若O点是△ABC三条中线的交点,以O点为旋转中心,旋转多少度后能与原来的图形重合?
,D、E、F分别是CA、BC、AB延长线上的点,且AD=AC,CE=CB,AB=BF,连结DE、EF、FD,试问△DEF是什么三角形?若O点是△ABC三条中线的交点,以O点为旋转中心,旋转多少度后能与原来的图形重合?
答案:
解析:
解析:
|
解:已知AD=AC,CE=CB,AB=BF 所以AD=CE=BF,DC=AF=BE 如题图所示,△DCE与△FAD与△EBF,将其中任何一个三角形先平移,后旋转都能完全重合 所以DE=DF=EF 因此△DEF为等边三角形 此图形是一个旋转对称图形,绕O点旋转 说明:本题涉及正三角形的外角、平移、旋转及旋转对称图形等知识,引导同学们大胆猜想、主动探究,提高综合运用知识的能力. |

练习册系列答案
相关题目
 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF. 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长. 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.