Question

【题目】如图1，矩形纸片ABCD的边长AB=4cm，AD=2cm．同学小明现将该矩形纸片沿EF折痕，使点A与点C重合，折痕后在其一面着色（如图2），观察图形对比前后变化，回答下列问题：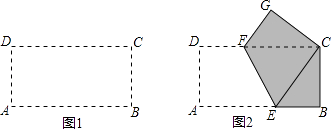

（1）GFFD：（直接填写=、＞、＜）
（2）判断△CEF的形状，并说明理由；
（3）小明通过此操作有以下两个结论：
①四边形EBCF的面积为4cm2
②整个着色部分的面积为5.5cm2
运用所学知识，请论证小明的结论是否正确．

Answer 1

【答案】
（1）=
（2）解：△CEF是等腰三角形．

∵矩形ABCD，

∴AB∥CD，

∴∠AEF=∠CFE，

由翻折的性质，∠AEF=∠FEC，

∴∠CFE=∠FEC，

∴CF=CE，

故△CEF为等腰三角形

（3）解：①由翻折的性质，AE=EC，

∵EC=CF，

∴AE=CF，

∴S四边形EBCF= （EB+CF）BC= ABBC= ×4×2× =4cm2；

②设GF=x，则CF=4﹣x，

∵∠G=90°，

∴x2+22=（4﹣x）2，

解得x=1.5，

∴SGFC= ×1.5×2=1.5，

S着色部分=1.5+4=5.5；

综上所述，小明的结论正确

【解析】解：（1）由翻折的性质，GD=FD；
【考点精析】本题主要考查了矩形的性质和翻折变换（折叠问题）的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．