题目内容
【题目】如图，已知DE∥BC，CD是∠ACB的平分线，∠B=70°，∠ACB=50°，求∠EDC和∠BDC的度数．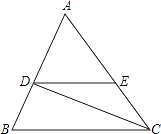 
【答案】解：∵CD是∠ACB的平分线，∠ACB=50°，
∴∠BCD= 
∠ACB=25°，
∵DE∥BC，
∴∠EDC=∠DCB=25°，∠BDE+∠B=180°，
∵∠B=70°，
∴∠BDE=110°，
∴∠BDC=∠BDE﹣∠EDC=110°﹣25°=85°．
∴∠EDC=25°，∠BDC=85°
【解析】由CD是∠ACB的平分线，∠ACB=50°，根据角平分线的性质，即可求得∠DCB的度数，又由DE∥BC，根据两直线平行，内错角相等，即可求得∠EDC的度数，根据两直线平行，同旁内角互补，即可求得∠BDE的度数，即可求得∠BDC的度数．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
【题目】为了建设“书香校园”，某班开展捐书活动班长将本班44名学生捐书情况统计如下：
捐书本数 | 2 | 3 | 4 | 5 | 8 | 10 |
捐书人数 | 2 | 5 | 12 | 21 | 3 | 1 |
该组数据捐书本数的众数和中位数分别为（ ）
A. 5，5B. 21，8C. 10，4.5D. 5，4.5
