��Ŀ����
����Ŀ���ӻ���ij��ѧ������1������ѧ��ȤС��Ϊ�˽�ȫУ800������ѧ���ġ����б�ҵѡ����ѧ�;�ҵ��������ضԱ���50��ͬѧ�ǽ��е��飬����ȫ��ͬѧ�����3����Ҫ�۵㣺A���У�B�м���C��ҵ�������˵��飨Ҫ��ÿλͬѧֻѡ�Լ����Ͽɵ�һ��۵㣩�����Ƴ�������ͳ��ͼ����ͼ������ش��������⣺
��1���ð�ѧ��ѡ���� ���۵��������࣬������ ���ˣ�������ͳ��ͼ�У��ù۵��������������Բ�Ľ����� ���ȣ�
��2�������������Ƹ�У����ѧ��ѡ���м����۵��������
��3����֪�ð�ֻ��2λŮͬѧѡ��ҵ���۵㣬��������δӸù۵��У����ѡȡ2λͬѧ���е��飬��ôǡ��ѡ����2λŮͬѧ�ĸ����Ƕ��٣���������ͼ���б���������𣩣�

���𰸡���1��A���й۵㣮30�� 216����2��256�ˣ���3��![]() ��
��
��������
���⣨1��ȫ����������ѡ����A�������۵�İٷֱȼ��ɵõ�ѡ����A�������۵����������360������ѡ����A�������۵�İٷֱȼ��ɵõ�ѡ����A�������Ĺ۵��������������Բ�ĽǵĶ�����
��2����ȫУ�����꼶ѧ��������ѡ����B�м����۵�İٷֱȼ��ɹ��Ƹ�У����ѧ��ѡ�����м����۵��������
��3���ȼ�����ð�ѡ������ҵ���۵������Ϊ4�ˣ�����ж���2λŮͬѧ��2λ����ѡ������ҵ���۵㣬���б�չʾ12�ֵȿ��ܵĽ�������ҳ�����2Ů�Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�����������1���ð�ѧ��ѡ��A���й۵��������࣬����60%��50=30���ˣ���������ͳ��ͼ�У��ù۵��������������Բ�Ľ���60%��360��=216����
��2����800��32%=256���ˣ���
�����Ƹ�У����ѧ��ѡ�����м����۵������Լ��256�ˣ�
��3���ð�ѡ������ҵ���۵������=50����1-60%-32%��=50��8%=4���ˣ�����ð���2λŮͬѧ��2λ����ѡ������ҵ���۵㣬
�б����£�
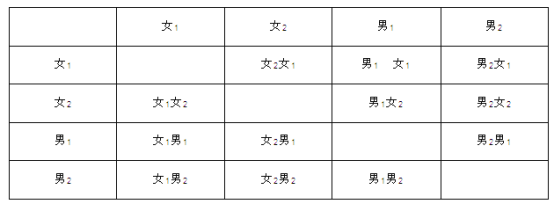
����12�ֵȿ��ܵĽ���������г���2Ů���������2�֣�
����ǡ��ѡ��2λŮͬѧ�ĸ���=![]() ��
��