题目内容
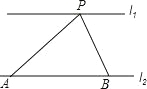
【题目】如图,直线l1∥l2,两直线之间的距离为2,A,B是直线l2上两点,AB=4,点P直线l1上一个动点,则∠APB的最大值为 .
【答案】90°.
【解析】
试题分析:结合已知条件作图如下,
 “以线段AB为直径作圆,圆与直线l1交于点P,在l1上任找一点P′(与点P不重合),连接AP′交圆于点C,连接BC”,根据线段AB为直径可得出∠APB=∠ACB=90°,再结合三角形外角的性质即可得出∠APB>∠AP′B,由此即可得出结论.∵AB=4,直线l1∥l2,两直线之间的距离为2,∴以线段AB为直径作圆,圆与直线l1交于点P,在l1上任找一点P′(与点P不重合),连接AP′交圆于点C,连接BC,如上图所示.∵线段AB为直径,∴∠APB=∠ACB=90°,∵∠ACB=∠AP′B+∠CBP′,∴∠APB=∠ACB>∠AP′B.∴当点P在线段AB的垂直平分线上时,∠APB最大,最大值为90°.故答案为:90°.
“以线段AB为直径作圆,圆与直线l1交于点P,在l1上任找一点P′(与点P不重合),连接AP′交圆于点C,连接BC”,根据线段AB为直径可得出∠APB=∠ACB=90°,再结合三角形外角的性质即可得出∠APB>∠AP′B,由此即可得出结论.∵AB=4,直线l1∥l2,两直线之间的距离为2,∴以线段AB为直径作圆,圆与直线l1交于点P,在l1上任找一点P′(与点P不重合),连接AP′交圆于点C,连接BC,如上图所示.∵线段AB为直径,∴∠APB=∠ACB=90°,∵∠ACB=∠AP′B+∠CBP′,∴∠APB=∠ACB>∠AP′B.∴当点P在线段AB的垂直平分线上时,∠APB最大,最大值为90°.故答案为:90°.

练习册系列答案
相关题目