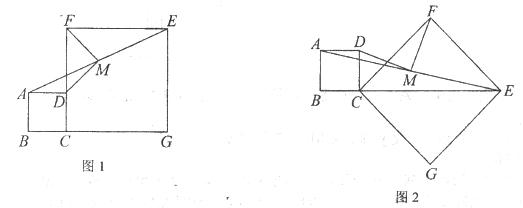
题目内容
如图,在 和
和 中,
中, ,
,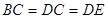 ,
, >
> ,
, ,点
,点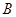 、
、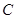 、
、 在直线
在直线 上,
上,

(1)按下列要求画图(保留画图痕迹):
①画出点 关于直线
关于直线 的对称点
的对称点 ,连接
,连接 、
、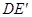 ;
;
②以点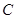 为旋转中心,将(1)中所得
为旋转中心,将(1)中所得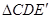 按逆时针方向旋转,使得
按逆时针方向旋转,使得 旋转后的线段
旋转后的线段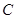
 与
与 重合,得到
重合,得到 (A),画出
(A),画出 .
.
(2)解决下面问题:
①线段 和线段
和线段 的位置关系是 .并说明理由.
的位置关系是 .并说明理由.
②求∠ 的度数.
的度数.
 和
和 中,
中, ,
,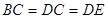 ,
, >
> ,
, ,点
,点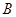 、
、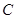 、
、 在直线
在直线 上,
上,
(1)按下列要求画图(保留画图痕迹):
①画出点
 关于直线
关于直线 的对称点
的对称点 ,连接
,连接 、
、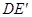 ;
;②以点
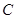 为旋转中心,将(1)中所得
为旋转中心,将(1)中所得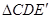 按逆时针方向旋转,使得
按逆时针方向旋转,使得 旋转后的线段
旋转后的线段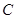
 与
与 重合,得到
重合,得到 (A),画出
(A),画出 .
.(2)解决下面问题:
①线段
 和线段
和线段 的位置关系是 .并说明理由.
的位置关系是 .并说明理由.②求∠
 的度数.
的度数.(1)①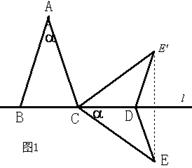 ②
②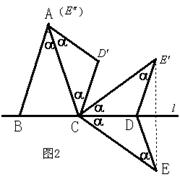 (2)①平行,理由见解析②36°
(2)①平行,理由见解析②36°
 ②
② (2)①平行,理由见解析②36°
(2)①平行,理由见解析②36°(1)①如图1所示………(2分)②如图2所示………(6分)
(2)①平行.理由:∵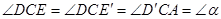 ,
,
∴ ,∴
,∴ ∥
∥ ………………………………………(9分)
………………………………………(9分)
②∵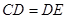 ,∴
,∴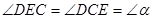 .
.
根据作图可知: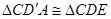 ,∴
,∴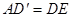 ,
, .
.
又∵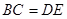 ,∴
,∴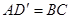 .由①知
.由①知 ∥
∥ ,∴四边形
,∴四边形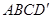 是等腰梯形.
是等腰梯形.
又∵ ,∴
,∴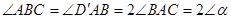 .
.
在 中,∵
中,∵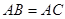 ,∴
,∴ ,
,
∴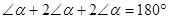 ,∴
,∴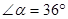 ……………………………………(12分)
……………………………………(12分)
(1)①从点E向直线l引垂线,并延长相同单位,找到它的对称点E′,连接CE′、DE′;
②把CE′逆时针旋转与CA重合,再把CD逆时针旋转相同的角度,得到CD′,连接D′E″得到△CD′E″.
(2)①等量代换利用平行线的判定即可证明是平行.
②利用等腰梯形的性质及三角形的内角和是180度来计算.
(2)①平行.理由:∵
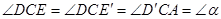 ,
,∴
 ,∴
,∴ ∥
∥ ………………………………………(9分)
………………………………………(9分)②∵
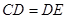 ,∴
,∴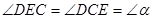 .
.根据作图可知:
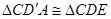 ,∴
,∴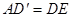 ,
, .
.又∵
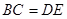 ,∴
,∴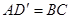 .由①知
.由①知 ∥
∥ ,∴四边形
,∴四边形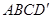 是等腰梯形.
是等腰梯形.又∵
 ,∴
,∴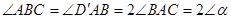 .
.在
 中,∵
中,∵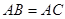 ,∴
,∴ ,
,∴
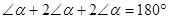 ,∴
,∴ ……………………………………(12分)
……………………………………(12分)(1)①从点E向直线l引垂线,并延长相同单位,找到它的对称点E′,连接CE′、DE′;
②把CE′逆时针旋转与CA重合,再把CD逆时针旋转相同的角度,得到CD′,连接D′E″得到△CD′E″.
(2)①等量代换利用平行线的判定即可证明是平行.
②利用等腰梯形的性质及三角形的内角和是180度来计算.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )
方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )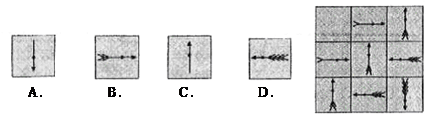
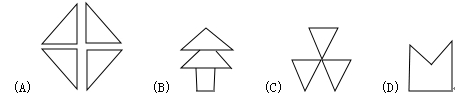
 则电子表的实际读数________.
则电子表的实际读数________. 



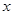 轴对称的两个三角形是( ).
轴对称的两个三角形是( ). .①和②;
.①和②;  .②和③;
.②和③;  .①和③;
.①和③;  .②和④.
.②和④.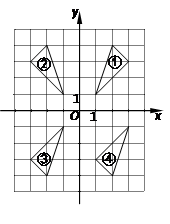
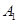 ,则点
,则点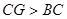 ),B、C、G在同一条直线上,M为线段AE的中点。探究:线段MD、MF的关系,并证明。
),B、C、G在同一条直线上,M为线段AE的中点。探究:线段MD、MF的关系,并证明。