题目内容
a，b，c均不为0，若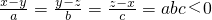
，则P（ab，bc）不可能在
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
A
分析：应根据abc＜0，得到这三个字母可能的符号，推出不存在的结论，进而得到不可能在的象限．
解答：∵abc＜0．
∴a，b，c中至少有一个是负数，另两个同号，
可知三个都是负数或两正数，一个是负数，
当三个都是负数时：若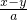
=abc，则x-y=a2bc＞0，即x＞y，同理可得：y＞z，z＞x这三个式子不能同时成立，即a，b，c不能同时是负数．则P（ab，bc）不可能在第一象限．
故选A．
点评：确定一个点所在象限，就是确定点的坐标的符号．
分析：应根据abc＜0，得到这三个字母可能的符号，推出不存在的结论，进而得到不可能在的象限．
解答：∵abc＜0．
∴a，b，c中至少有一个是负数，另两个同号，
可知三个都是负数或两正数，一个是负数，
当三个都是负数时：若
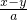=abc，则x-y=a2bc＞0，即x＞y，同理可得：y＞z，z＞x这三个式子不能同时成立，即a，b，c不能同时是负数．则P（ab，bc）不可能在第一象限．故选A．
点评：确定一个点所在象限，就是确定点的坐标的符号．
练习册系列答案
相关题目
定义运算符号“﹡”的意义为：a﹡b=
（其中a、b均不为0）．下面有两个结论：（1）运算“﹡”满足交换律；（2）运算“﹡”满足结合律．其中（ ）
| a+b |
| ab |
| A、只有（1）正确 |
| B、只有（2）正确 |
| C、（1）和（2）都正确 |
| D、（1）和（2）都不正确 |