题目内容
【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.

(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
【答案】(1)证明见解析(2)AG⊥BE(3)证明见解析
【解析】
(1)根据正方形的性质得DA=DC,∠ADB=∠CDB=45°,则可根据“SAS”证明△ADG≌△CDG,所以∠DAG=∠DCG;
(2)根据正方形的性质得AB=DC,∠BAD=∠CDA=90°,根据“SAS”证明△ABE≌△DCF,则∠ABE=∠DCF,由于∠DAG=∠DCG,所以∠DAG=∠ABE,然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°,于是可判断AG⊥BE;
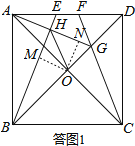
(3)如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,证明△AON≌△BOM,可得四边形OMHN为正方形,因此HO平分∠BHG结论成立.
(1)证明:∵四边形ABCD为正方形,
∴DA=DC,∠ADB=∠CDB=45°,
在△ADG和△CDG中,
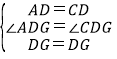 ,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG;
(2)解:AG⊥BE.理由如下:
∵四边形ABCD为正方形,
∴AB=DC,∠BAD=∠CDA=90°,
在△ABE和△DCF中,
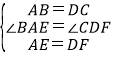 ,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
∵∠DAG=∠DCG,
∴∠DAG=∠ABE,
∵∠DAG+∠BAG=90°,
∴∠ABE+∠BAG=90°,
∴∠AHB=90°,
∴AG⊥BE;
(3)解:由(2)可知AG⊥BE.
如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.
∴∠MON=90°,
又∵OA⊥OB,
∴∠AON=∠BOM.
∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,
∴∠OAN=∠OBM.
在△AON与△BOM中,
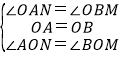 ,
,
∴△AON≌△BOM(AAS).
∴OM=ON,
∴矩形OMHN为正方形,
∴HO平分∠BHG.