题目内容
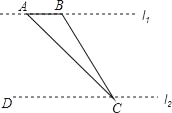
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,![]() 种纸片边长为
种纸片边长为![]() 的正方形,
的正方形,![]() 中纸片是边长为
中纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片是长为
种纸片是长为![]() 、宽为
、宽为![]() 的长方形.并用
的长方形.并用![]() 种纸片一张,
种纸片一张,![]() 种纸片一张,
种纸片一张,![]() 种纸片两张拼成如图2的大正方形.
种纸片两张拼成如图2的大正方形.
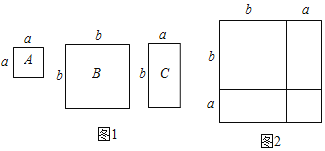
(1)请问两种不同的方法求图2大正方形的面积.
方法1:![]() ____________________;方法2:
____________________;方法2:![]() ________________________;
________________________;
(2)观察图2,请你写出下列三个代数式:![]() 之间的等量关系.
之间的等量关系.
_______________________________________________________;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②已知![]() ,则
,则![]() 的值是____.
的值是____.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ,②
,②![]()
【解析】
(1)依据正方形的面积计算公式即可得到结论;
(2)依据(1)中的代数式,即可得出(a+b)2,a2+b2,ab之间的等量关系;
(3)①依据a+b=5,可得(a+b)2=25,进而得出a2+b2+2ab=25,再根据a2+b2=11,即可得到ab=7;②设2020-a=x,a-2019=y,即可得到x+y=1,x2+y2=5,依据(x+y)2=x2+2xy+y2,即可得出xy=![]() =
=![]() ,进而得到
,进而得到![]() =
=![]() .
.
解:(1)图2大正方形的面积=![]() ,图2大正方形的面积=
,图2大正方形的面积=![]()
故答案为:![]() ,
,![]() ;
;
(2)由题可得![]() ,
,![]() ,
,![]() 之间的等量关系为:
之间的等量关系为:![]() 故答案为:
故答案为:![]() ;
;
(3)①![]()
![]()
![]()
②设2020-a=x,a-2019=y,则x+y=1,
∵![]() ,
,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy=![]() =-2,
=-2,
即![]() .
.

【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
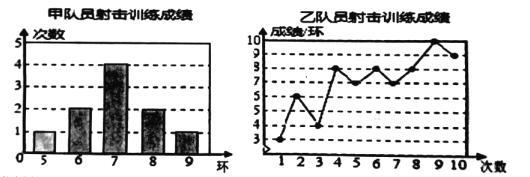
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?