Question

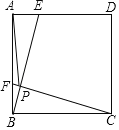
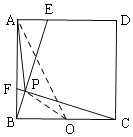
【题目】如图，点E、F是边长为4的正方形ABCD边AD、AB上的动点，且AF＝DE，BE交CF于点P，在点E、F运动的过程中，PA的最小值为（　　）

A.2B.2C.4﹣2D.2﹣2

Answer 1

【答案】D

【解析】

根据直角三角形斜边上的中线等于斜边的一半，取BC的中点O，连接OP、OA，然后求出OP＝CB＝2，利用勾股定理列式求出OA，然后根据三角形的三边关系可知当O、P、A三点共线时，AP的长度最小．

解：在正方形ABCD中，

∴AB＝BC，∠BAE＝∠ABC＝90°，

在△ABE和△BCF中，

∵，

∴△ABE≌△BCF（SAS），

∴∠ABE＝∠BCF，

∵∠ABE+∠CBP＝90°

∴∠BCF+∠CBP＝90°

∴∠BPC＝90°

如图，取BC的中点O，连接OP、OA，

则OP＝BC＝2，

在Rt△AOB中，OA＝，

根据三角形的三边关系，OP+AP≥OA，

∴当O、P、A三点共线时，AP的长度最小，

AP的最小值＝OA﹣OP＝﹣2．

故选：D．