题目内容
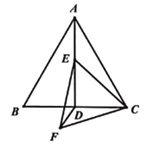
【题目】如图①,四边形![]() 和四边形
和四边形![]() 都是正方形,且
都是正方形,且![]() ,
,![]() ,正方形
,正方形![]() 固定,将正方形
固定,将正方形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角(
角(![]() ).
).

(1)如图②,连接![]() 、
、![]() ,相交于点
,相交于点![]() ,请判断
,请判断![]() 和
和![]() 是否相等?并说明理由;
是否相等?并说明理由;
(2)如图②,连接![]() ,在旋转过程中,当
,在旋转过程中,当![]() 为直角三角形时,请直接写出旋转角
为直角三角形时,请直接写出旋转角![]() 的度数;
的度数;
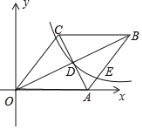
(3)如图③,点![]() 为边
为边![]() 的中点,连接
的中点,连接![]() 、
、![]() 、
、![]() ,在正方形
,在正方形![]() 的旋转过程中,
的旋转过程中,![]() 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
【答案】(1)相等,理由见解析;(2)![]() 和
和![]() ;(3)存在,最大值为
;(3)存在,最大值为![]() .
.
【解析】
(1)由四边形ABCD和四边形CEFG都是正方形知BC=CD,CF=CE,∠BCD=∠GCE=90°,从而得∠BCG=∠DCE,证△BCG≌△DCE得BG=DE;
(2)分两种情况求解可得;
(3)由![]() ,知当点P到BD的距离最远时,△BDP的面积最大,作PH⊥BD,连接CH、CP,则PH≤CH+CP,当P、C、H三点共线时,PH最大,此时△BDP的面积最大,据此求解可得.
,知当点P到BD的距离最远时,△BDP的面积最大,作PH⊥BD,连接CH、CP,则PH≤CH+CP,当P、C、H三点共线时,PH最大,此时△BDP的面积最大,据此求解可得.
(1)证明:相等
∵四边形![]() 和四边形
和四边形![]() 都是正方形,
都是正方形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ;
;
∴BG=DE
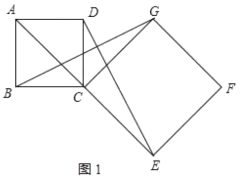
(2)如图1,∠ACG=90°时,旋转角![]() ;
;
如图2,当∠ACG=90°时,旋转角![]() ;
;
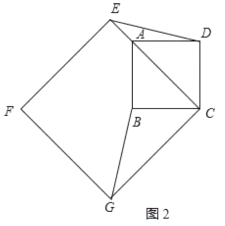
综上所述,旋转角![]() 的度数为45°或225°;
的度数为45°或225°;
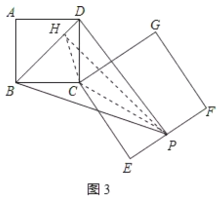
(3)存在
∵如图3,在正方形![]() 中,
中,![]() ,
,
∴![]() ,
,
∴当点![]() 到
到![]() 的距离最远时,
的距离最远时,![]() 的面积最大,
的面积最大,
作![]() ,连接
,连接![]() ,
,![]() ,则
,则![]()
当![]() 三点共线时,
三点共线时,![]() 最大,此时
最大,此时![]() 的面积最大.
的面积最大.
∵![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
∴![]()
此时![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.