题目内容
【题目】已知抛物线![]() 与x轴相交于不同的两点
与x轴相交于不同的两点![]() ,
,
(1)求![]() 的取值范围
的取值范围
(2)证明该抛物线一定经过非坐标轴上的一点![]() ,并求出点
,并求出点![]() 的坐标;
的坐标;
(3)当![]() 时,由(2)求出的点
时,由(2)求出的点![]() 和点
和点![]() 构成的
构成的![]() 的面积是否有最值,若有,求出最值及相对应的
的面积是否有最值,若有,求出最值及相对应的![]() 值;若没有,请说明理由.
值;若没有,请说明理由.
【答案】(1)![]() 且
且![]() ;(2)(3,4);(3)详见解析.
;(2)(3,4);(3)详见解析.
【解析】
试题分析:(1)根据根的判别式求出m的取值范围,注意![]() ;(2)令
;(2)令![]() ,得出
,得出![]() ,故过定点P(3,4);(3)利用韦达定理写出AB的长度
,故过定点P(3,4);(3)利用韦达定理写出AB的长度![]() ,再根据m的取值范围,求出
,再根据m的取值范围,求出![]() 的面积的最大值.
的面积的最大值.
试题解析:(1)根据已知可知
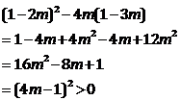
所以 ![]() 所以
所以![]()
所以m的取值范围为![]() 且
且![]() .
.
(2)令![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;所以抛物线过定点(-1,0),(3,4),因为(-1,0)在x轴上,所以抛物线一定经过非坐标轴上一点P,P的坐标为(3,4)
;所以抛物线过定点(-1,0),(3,4),因为(-1,0)在x轴上,所以抛物线一定经过非坐标轴上一点P,P的坐标为(3,4)
(3)设A,B的坐标为![]() ,则
,则![]()
![]()
![]()
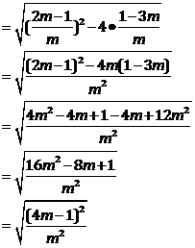
因为 ,所以
,所以![]() ,所以
,所以![]() =2AB
=2AB![]() =
=![]()
![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以当
,所以当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() =
=![]()
考点:二次函数综合题.

练习册系列答案
相关题目