��Ŀ����
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�ڵ�A����1��0����B��3��0������y���ཻ�ڵ�C��0����3����
��1����˶��κ����Ľ���ʽ��
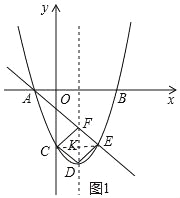
��2���������ߵĶ���ΪD����E���������ϣ������C���������ߵĶԳ���Գƣ�ֱ��AE���Գ����ڵ�F�����ж��ı���CDEF����״����˵�����ɣ�
��3������M��x���ϣ���P���������ϣ��Ƿ������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ������ڣ���ֱ��д����������Ҫ��ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
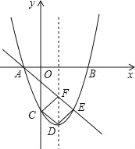
���𰸡���1�������ߵĽ���ʽΪy=x2��2x��3��
��2���ı���EFCD����������
��3����P��������1+![]() ��2����1��
��2����1��![]() ��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
��������
�����������1�����ô���ϵ�������ɽ�����⣮
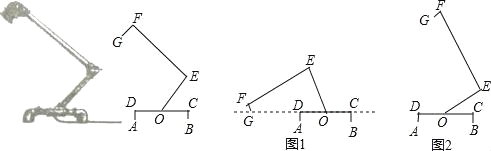
��2�������ı���EFCD�������Σ���ͼ1�У�����CE��DF���ڵ�K�����E��F��D��C�ĵ����ֻ꣬Ҫ֤��DF��CE��DF=CE��KC=KE��KF=KD����֤����
��3����ͼ2�У�������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ����ݵ�P��������Ϊ2��2�����ɽ�����⣮
�����������1����A����1��0����B��3��0����C��0����3������y=ax2+bx+c�� ��
��
���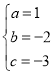 ���������ߵĽ���ʽΪy=x2��2x��3��
���������ߵĽ���ʽΪy=x2��2x��3��
��2�������ı���EFCD�������Σ�
���ɣ���ͼ1�У�����CE��DF���ڵ�K��
��y=��x��1��2��4��������D��1��4������C��E���ڶԳ���Գƣ�C��0����3����
��E��2����3������A����1��0������ֱ��AE�Ľ���ʽΪy=kx+b��
��![]() �����
�����![]() ��
��
��ֱ��AE�Ľ���ʽΪy=��x��1��
��F��1����2����
��CK=EK=1��FK=DK=1��
���ı���EFCD��ƽ���ı��Σ�
����CE��DF��CE=DF��
���ı���EFCD�������Σ�
��3����ͼ2�У�������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�

�������P��������Ϊ2��2��
��y=2ʱ��x2��2x��3=2�����x=1��![]() ��
��
�ɵ�P1��1+![]() ��2����P2��1-
��2����P2��1-![]() ��2����
��2����
��y=��2ʱ��x=0���ɵ�P3��0����2����
����������P��������1+ ![]() ��2����1��
��2����1��![]() ��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
��2����0����2��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�