题目内容
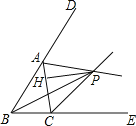
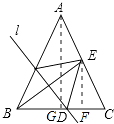
【题目】如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为 . 
【答案】13
【解析】解:过点A作AG⊥BC于点G,
∵AB=AC,BC=24,tanC=2,
∴ ![]() =2,GC=BG=12,
=2,GC=BG=12,
∴AG=24,
∵将△ABC沿直线l翻折后,点B落在边AC的中点处,
过E点作EF⊥BC于点F,
∴EF= ![]() AG=12,
AG=12,
∴ ![]() =2,
=2,
∴FC=6,
设BD=x,则DE=x,
∴DF=24﹣x﹣6=18﹣x,
∴x2=(18﹣x)2+122,
解得:x=13,
则BD=13.
所以答案是:13.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目
【题目】为了支持国货,哈市某手机卖场计划用![]() 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌![]() 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表:
|
|
| |
进价(元/部) |
|
|
|
售价(元/部) |
|
|
|
若该手机卖场同时购进两种不同型号的手机![]() 台,
台,![]() 万元刚好用完.
万元刚好用完.
(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润![]() 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?