题目内容
【题目】在平面直角坐标系中,将抛物线C1:y=x2﹣2x向左平移2个单位,向下平移3个单位得到新抛物线C2.
(1)求新抛物线C2的表达式;
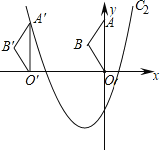
(2)如图,将△OAB沿x轴向左平移得到△O′A′B′,点A(0,5)的对应点A′落在平移后的新抛物线C2上,求点B与其对应点B′的距离.
【答案】(1)y=(x+1)2﹣4;(2)4个单位.
【解析】
(1)根据平移规律“左加右减,上加下减”解答;
(2)把y=5代入抛物线C2求得相应的x的值,即可求得点A′的坐标,根据平移的性质,线段AA′的长度即为所求.
解:
(1)由抛物线C1:y=x2﹣2x=(x﹣1)2﹣1知,将其向左平移2个单位,向下平移3个单位得到新抛物线C2的表达式是:y=(x﹣1+2)2﹣1﹣3,即y=(x+1)2﹣4;
(2)由平移的性质知,点A与点A′的纵坐标相等,
所以将y=5代入抛物线C2,得(x+1)2﹣4=5,则x=﹣4或x=2(舍去)
所以AA′=4,
根据平移的性质知:BB′=AA′=4,即点B与其对应点B′的距离为4个单位.

练习册系列答案
相关题目
【题目】某水果公司以2.2元/千克的成本价购进![]() 苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果损坏的频率 | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为______精确到0.1),据此,若公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为______元/千克.