题目内容
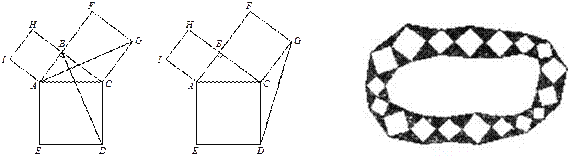
【题目】如图,在△ABC中,∠ABC=90°,分别以边AB、BC、CA向△ABC外作正方形ABHI、正方形BCGF、正方形CAED,连接GD,AG,BD. (提示:正方形的四条边相等,四个角均为直角,可直接运用。)
(1)如图1,求证:AG=BD.
(2)如图2,试说明:S△ABC=S△CDG.
(3)园林小路,曲径通幽,如图3所示,小路由白色的正方形大理石和黑色的三角形大理石铺成,已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地 平方米.(不用写过程)
【答案】(1)见解析;(2)见解析;(3)a+2b
【解析】试题分析:(1)由正方形的性质就可以得出△ACG≌△DCB,就可以得出结论;
(2)延长DC交GF于H,证明△BMC≌△GNC,就可以得出BM=GN,就可以得出结论.
(3)同(2)道理知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,求出这条小路一共占地多少平方米.
试题解析:(1)∵四边形ABHI、四边形BCGF和四边形CAED都是正方形,∴AB=BH=HI=AI,BC=CG=GF=BF,AE=DE=CD=AC,∠H=∠I=∠E=∠F=∠IAB=∠ABH=∠FBC=∠BCG=∠FGC=∠BAC=∠ACD=90°.
∴∠ACD+∠ACB=∠BCG+∠ACB,
∴∠DCB=∠ACG.
在△ACG和△DCB中,
 ,
,
∴△ACG≌△DCB(SAS),
∴AG=BD;
(2)如图,作BM⊥AC于M,GN⊥DC的延长于点N.

∴∠BMC=∠N=90°
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
在△BMC和△GNC中,
 ,
,
∴△BMC≌△GNC(AAS),
∴BM=GN,
∴![]() ACBM=
ACBM=![]() DCGN,
DCGN,
∵S△ABC=![]() ACBM,S△DCG=
ACBM,S△DCG=![]() DCGN,
DCGN,
∴S△ABC=S△CDG.
(3)由(2)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和。
∴这条小路的面积为(a+2b)平方米。


