题目内容
【题目】如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且点A在x轴上，点B的横坐标为2，连结AM、BM．
（1）求抛物线的函数关系式；
（2）判断△ABM的形状，并说明理由；
（3）把抛物线与直线y=x的交点称为抛物线的不动点．若将（1）中抛物线平移，使其顶点为（m，2m），当m满足什么条件时，平移后的抛物线总有不动点．
【答案】（1）抛物线解析式为y=x2﹣1；
（2）△ABM为直角三角形，理由见解析；
（3）当m≤
时，平移后的抛物线总有不动点．
【解析】
试题分析：（1）由条件可分别求得A、B的坐标，设出抛物线解析式，利用待定系数法可求得抛物线解析式；
（2）结合（1）中A、B、C的坐标，根据勾股定理可分别求得AB、AM、BM，可得到AB2+AM2=BM2，可判定△ABM为直角三角形；
（3）由条件可写出平移后的抛物线的解析式，联立y=x，可得到关于x的一元二次方程，根据根的判别式可求得m的范围．
试题解析：（1）∵A点为直线y=x+1与x轴的交点，∴A（﹣1，0），又B点横坐标为2，代入y=x+1可求得y=3，∴B（2，3），∵抛物线顶点在y轴上，∴可设抛物线解析式为y=ax2+c，
把A、B两点坐标代入可得
，解得
，∴抛物线解析式为y=x2﹣1；
（2）△ABM为直角三角形．理由如：
由（1）抛物线解析式为y=x2﹣1可知M点坐标为（0，﹣1），∴AM=
，AB=3
，BM=2
，
∴AM2+AB2=2+18=20=BM2，∴△ABM为直角三角形；
（3）当抛物线y=x2﹣1平移后顶点坐标为（m，2m）时，其解析式为y=（x﹣m）2+2m，即y=x2﹣2mx+m2+2m，
联立y=x，可得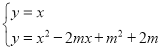
，消去y整理可得x2﹣（2m+1）x+m2+2m=0，
∵平移后的抛物线总有不动点，
∴方程x2﹣（2m+1）x+m2+2m=0总有实数根，
∴△≥0，即（2m+1）2﹣4（m2+2m）≥0，
解得m≤
，即当m≤时，平移后的抛物线总有不动点．
