��Ŀ����
����Ŀ����֪������ABCD�У���ABC=60�㣬�Խ���AC��BD�ཻ�ڵ�O����E���߶�BD��һ���㣨�����B��D�غϣ�������AE����AEΪ����AE���Ҳ�������AEFG���ҡ�AEF=60�㣮
��1����ͼ1������F�����߶�BD�ϣ����жϣ��߶�EF���߶�DF��������ϵ��.
��2����ͼ2��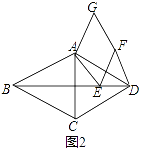
����F�����߶�BD�ϣ������������䣬��1���еĽ����Ƿ���Ȼ������������жϲ�����֤����
��3������C��E��G������ͬһֱ���ϣ������������䣬��ֱ��д���߶�BE���߶�BD����ϵ��
���𰸡�
��1��
�⣺��ͼ1������AF��

���ı���ABCD�����Σ�
��AC��BD����ABO= ![]() ��ABC=30�㣬
��ABC=30�㣬
���OAE=��OAF=30�㣬
���DAF=30��=��ADO��
��AF=FD��
��AF=EF��
��EF=FD��
�ߡ�AEF=60�㣬
���BAE=30��=��ABO��
��AE=BE
��2��
�⣺��������ͼ3��
����CE��AF��

���ı���ABCD�����Σ��ı���AEFG�����Σ�
��AD=CD��AE=EF��BD��ֱƽ��AC����ABC=��ADC=60�㣬
���ADC=��AEF=60�㣬
���ACD�͡�AEF�ǵȱ������Σ�
��AC=AD��AE=AF=EF����CAD=��EAF=60�㣬
���CAE=��DAF��
�ڡ�ACE�͡�ADF�У�  ��
��
��ACE�ա�ADF��
��EC=DF��
��BD��ֱƽ��AC��
��EC=AE��
��DF=AE=EF
��3��
�⣺��AE=CE��
���ACE=��CAE��
�ߵ�C��E��G��ͬһ��ֱ���ϣ�
���AEG=2��CAE=30�㣬
���CAE=15�㣬
�ߡ�BAO=60��㣬
���BAE=75�㣬
�ߡ�ABO= ![]() ��ABC=30�㣬
��ABC=30�㣬
���AEB=75��=��BAE��
��BE=AB��
��Rt��AOB�У���ABO=30�㣬
��cos��ABO= ![]() =
= ![]() ��
��
��OB= ![]() AB=
AB= ![]() BE��
BE��
��BD=2OB= ![]() BE
BE
����������1�����������ε����ʵó���ABO=��ADO=30�㣬AC��BD�����������FAD=30�㼴�ɵó����ۣ���2�����жϳ���ACD�͡�AEF�ǵȱ������Σ������ó���CAE=��DAF�������жϳ���ACE�ա�ADF�����ɵó����ۣ���3���������CAE=15�㣬�����жϳ�BE=AB�����ҳ�OB��AB�Ĺؼ����������ɵó����ۣ�

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�