题目内容
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE.
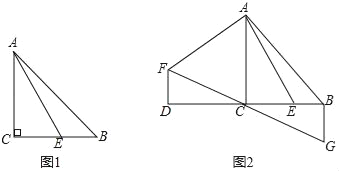
(1)如图1,当∠BAE=15°,CE=![]() 时,求AB的长.
时,求AB的长.
(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
【答案】(1)3![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)、根据题意得出△ABC为等腰直角三角形,根据题意得出∠CAE=30°,从而求出AE的长度,然后根据Rt△ACE的性质求出BC的长度,从而得出AB的长度;(2)、连接AD,线段AE绕点A顺时针旋转90°得线段AF,根据旋转的性质得出△ADF和△ABE全等,从而证明△BCG和△DCF全等,从而得出答案.
详解:(1)∵∠ACB=90°,AC=BC,∴△ABC是等腰直角三角形,∴∠BAC=45°,∠BAE=15°,
∴∠CAE=30°,∵CE=![]() ,∴Rt△ACE中,AE=2CE=2
,∴Rt△ACE中,AE=2CE=2![]() ,
,
∴由勾股定理可得,AC=![]() =3, ∴BC=3,
=3, ∴BC=3,
∴Rt△ABC中,由勾股定理可得,AB=![]() =3
=3![]() ;
;
(2)如图所示,连接AD,
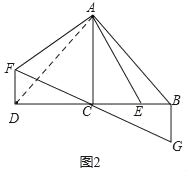
线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°, ∵AC⊥BD,DC=BC,
∴AD=AB,∠ABE=∠ADC=45°,又∵DF⊥DC,∴∠ADF=45°=∠ABE,
∵∠AFD+∠AED=180°=∠AEB+∠AED, ∴∠AFD=∠AEB, ∴△ADF≌△ABE,
∴DF=BE, ∵BG⊥BC,∴∠CBG=∠CDF=90°, 又∵BC=DC,∠BCG=∠DCF,
∴△BCG≌△DCF,∴DF=BG, ∴BG=BE.

【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度 | 电价/(元/度) |
不超过 |
|
超过 |
|
超过 |
|
解答下列问题:
(1)某居民![]() 月份用电量为
月份用电量为![]() 度,请问该居民
度,请问该居民![]() 月应缴电费多少元?
月应缴电费多少元?
(2)设某月的用电量为![]() 度
度![]() ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用![]() 表示) .
表示) .
(3)某居民![]() 月份缴电费
月份缴电费![]() 元,求该居民
元,求该居民![]() 月份的用电量.
月份的用电量.
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 6 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |

请结合图表完成下列各题:
(1)求表中a的值;(2)请把频数分布直方图补充完整;
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.