题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,BC=1,AC=![]() .
.
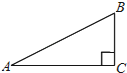
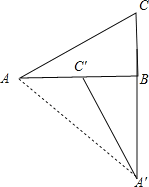
(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
【答案】(1)见解析;(2)2![]()
【解析】
试题分析:(1)在BA上截取BC′=BC,延长CB到A′使BA′=BA,然后连结A′C′,则△A′BC′满足条件;
(2)先利用勾股定理计算出AB=2,再利用旋转的性质得BA=BA′,∠ABA′=90°,然后根据等腰直角三角形的性质计算AA′的长即可.
解:(1)如图,△A′BC′为所作;
(2)∵∠ABC=90°,BC=1,AC=![]() ,
,
∴AB=![]() =2,
=2,
∵△ABC沿逆时针方向旋转90°得到△A′BC′,
∴BA=BA′,∠ABA′=90°,
∴△ABA′为等腰直角三角形,
∴AA′=![]() AB=2
AB=2![]() .
.

练习册系列答案
相关题目