ћвƒњƒЏ»Ё
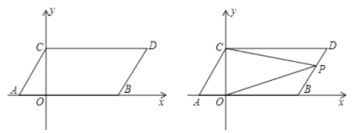
°Њћвƒњ°њ‘Џ°чABC÷–£ђAB£љ12£ђAC£љBC£љ10£ђљЂ°чABC»∆µгA∞іЋ≥ ±’лЈљѕт–э„™£ђµ√µљ°чADE£ђ–э„™љ«ќ™¶Ѕ(0°г<¶Ѕ<180°г)£ђµгBµƒґ‘”¶µгќ™D£ђµгCµƒґ‘”¶µгќ™E£ђЅђљ”BD£ђBE£Ѓ
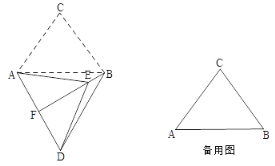
£®1£©»зЌЉ£ђµ±¶Ѕ£љ60°г ±£ђ—”≥§BEљїAD”ЏµгF£Ѓ
Ґў«у÷§£Ї°чABD «µ»±я»эљ«–ќ£ї
ҐЏ«у÷§£ЇBF°ЌAD£ђAF£љDF£ї
Ґџ«л÷±љ”–і≥цBEµƒ≥§£Ѓ
£®2£©‘Џ–э„™єэ≥ћ÷–£ђєэµгD„чDGіє÷±”Џ÷±ѕяAB£ђіє„гќ™G£ђЅђљ”CE£ђµ±°ѕDAG£љ°ѕACB£ђ«“ѕяґќDG”лѕяґќAEќёєЂє≤µг ±£ђ«л÷±љ”–і≥цBE£ЂCEµƒ÷µ£Ѓ
°Њір∞Є°њ£®1£©Ґў÷§√чЉыљвќц£їҐЏ÷§√чЉыљвќц£їҐџ BE£љ6![]() £≠8£ї£®2£©BE£ЂCE£љ26 £Ѓ
£≠8£ї£®2£©BE£ЂCE£љ26 £Ѓ
°Њљвќц°њ
£®1£©Ґў”…–э„™–‘÷ ÷™AB=AD£ђ°ѕBAD=60°гЉіњ…µ√÷§£ї
ҐЏ”…BA=BD°ҐEA=EDЄщЊЁѕяґќіє÷±∆љЈ÷ѕяµƒ–‘÷ Љіњ…µ√÷§£ї
ҐџЈ÷±р«у≥цBF°ҐEFµƒ≥§Љіњ…µ√£ї
£®2£©”…°ѕACB+°ѕBAC+°ѕABC=180°г°Ґ°ѕDAG+°ѕDAE+°ѕBAE=180°г°Ґ°ѕDAG=°ѕACB°Ґ°ѕDAE=°ѕBACµ√°ѕBAE=°ѕBAC«“AE=AC£ђЄщЊЁ»эѕяЇѕ“їњ…µ√CE°ЌAB°ҐAC=10°ҐAH=6£ђЉћґш÷™CE=2CH=16°ҐBE=10£ђЉіњ…µ√ір∞Є£Ѓ
£®1£©Ґў°я°чABC»∆µгAЋ≥ ±’лЈљѕт–э„™60°гµ√µљ°чADE£ђ
°аAB=AD£ђ°ѕBAD=60°г£ђ
°а°чABD «µ»±я»эљ«–ќ£ї
ҐЏ”…Ґўµ√°чABD «µ»±я»эљ«–ќ£ђ
°аAB=BD£ђ
°я°чABC»∆µгAЋ≥ ±’лЈљѕт–э„™60°гµ√µљ°чADE£ђ
°аAC=AE£ђBC=DE£ђ
”÷°яAC=BC£ђ
°аEA=ED£ђ
°аµгB°ҐE‘ЏADµƒѕяґќіє÷±∆љЈ÷ѕя…ѕ£ђ
°аBE «ADµƒѕяґќіє÷±∆љЈ÷ѕя£ђ
°яµгF‘ЏBEµƒ—”≥§ѕя…ѕ£ђ
°аBF°ЌAD£ђAF=DF£ї
Ґџ”…ҐЏ÷™BF°ЌAD£ђAF=DF£ђ
°аAF=DF=6£ђ
°яAE=AC=10£ђ
°аEF=8£ђ
°я‘Џµ»±я»эљ«–ќABD÷–£ђBF=![]() £ђ
£ђ
°аBE=BF©БEF=![]() £ї
£ї
£®2£©»зЌЉЋщ Њ£ђ
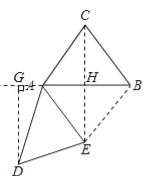
°я°ѕDAG=°ѕACB£ђ°ѕDAE=°ѕBAC£ђ
°а°ѕACB+°ѕBAC+°ѕABC=°ѕDAG+°ѕDAE+°ѕABC=180°г£ђ
”÷°я°ѕDAG+°ѕDAE+°ѕBAE=180°г£ђ
°а°ѕBAE=°ѕABC£ђ
°яAC=BC=AE£ђ
°а°ѕBAC=°ѕABC£ђ
°а°ѕBAE=°ѕBAC£ђ
°аAB°ЌCE£ђ«“CH=HE=![]() CE£ђ
CE£ђ
°яAC=BC£ђ
°аAH=BH=![]() AB=6£ђ
AB=6£ђ
°аCH=![]()
‘тCE=2CH=16£ђBE=10£ђ
°аBE+CE=10+16=26£Ѓ