题目内容
【题目】在△ABC中，角A，B，C的对边分别为，且满足 
．
（1）求角A的大小；
（2）若D为BC上一点，且 
，求a．
【答案】
（1）解：由 
，则（2c﹣b）cosA=acosB，
由正弦定理可知： 
= 
= 
=2R，则a=2RsinA，b=2RsinB，c=2RsinC，
∴（2sinC﹣sinB）cosA=sinAcosB，
整理得：2sinCcosA﹣sinBcosA=sinAcosB，
由A=π﹣（B+C），则sinA=sin[π﹣（B+C）]=sin（B+C），
即2sinCcosA=sin（A+B）=sinC，
由sinC≠0，则cosC= 
，即A= 
，
∴角A的大小
（2）解：过D作DE∥AB于E，则△ADE中，ED= 
AC=1，∠DEA= 
，
由余弦定理可知AD2=AE2+ED2﹣2AEEDcos ，
又AC=3，A= ，则△ABC为直角三角形，
∴a=BC=3 
，
∴a的值为3 ．
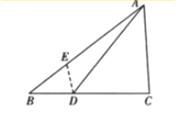
【解析】（1）由题意根据正弦定理求得∴（2sinC﹣sinB）cosA=sinAcosB，由A=π﹣（B+C），根据诱导公式及两角和正弦公式，即可求得A的值；（2）过D作DE∥AB于E，则△ADE中，ED= AC=1，∠DEA= ，由余弦定理可知△ABC为直角三角形，a=BC=3 ．
【题目】某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：
网购达人 | 非网购达人 | 合计 | |
男性 | 30 | ||
女性 | 12 | 30 | |
合计 | 60 |
若网购金额超过2千元的顾客称为“网购达人”，网购金额不超过2千元的顾客称为“非网购达人”．
（Ⅰ）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（Ⅱ）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定12人，若需从这12人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．
（参考公式： 
，其中n=a+b+c+d）
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】已知f（x）=x2（1nx﹣a）+a，则下列结论中错误的是（ ）
A.a＞0，x＞0，f（x）≥0
B.a＞0，x＞0，f（x）≤0
C.a＞0，x＞0，f（x）≥0
D.a＞0，x＞0，f（x）≤0
