题目内容
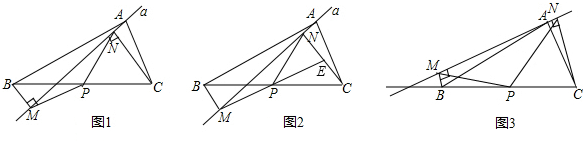
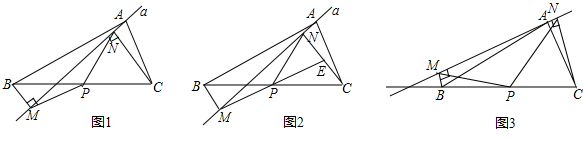
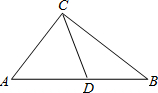
如图1,在Rt![]() 中,
中,![]() 点D在边AB上运动,DE平分
点D在边AB上运动,DE平分![]() 交边BC于点E,EM⊥BD垂足为
交边BC于点E,EM⊥BD垂足为![]() ,垂足为N.
,垂足为N.
(1)当AD=CD时,试说明![]() ;
;
(2)探究:AD为何值时,![]() 与
与![]() 相似?
相似?
 |
(1)证明:![]()
![]() (1分)
(1分)
又∵DE是∠BDC的平分线
∴∠BDC=2∠BDE
∴∠DAC=∠BDE (2分)
∴DE∥AC (4分)
(2)解:(Ⅰ)当![]() 时,得
时,得![]()
∴BD=DC
 ∵DE平分∠BDC
∵DE平分∠BDC
∴DE⊥BC,BE=EC.
∴∠DEB=∠ACB=90°,又∵∠B=∠B ∴△BDE∽△BAC
∴![]() 即
即![]()
∴AD=5 (8分)
(Ⅱ)当![]() 时,得
时,得![]() ∴EN∥BD
∴EN∥BD
又∵EN⊥CD ∴BD⊥CD即CD是△ABC斜边上的高
由三角形面积公式得AB·CD=AC·BC ∴CD=![]() (10分)
(10分)
∴![]() (11分)
(11分)
综上,当AD=5或![]() 时,△BME与△CNE相似. (12分)
时,△BME与△CNE相似. (12分)

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

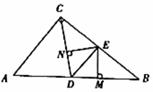
 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
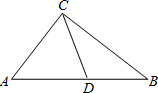
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD= .(此定理在解决下面的问题中要用到)
.(此定理在解决下面的问题中要用到)