题目内容
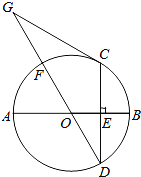
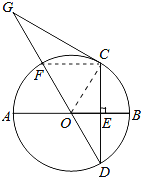
【题目】如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
(1)求证:![]() =
=![]() .
.
(2)若CD=6,求GF的长.
【答案】(1)证明见解析;(2)GF= 2![]() .
.
【解析】
试题分析:(1)只要证明∠COF=∠COV=60°即可.
(2)首先证明GF=CF,再在RT△CFD中利用勾股定理即可解决.
解:(1)如图,连接OC、CF.
∵AB是直径,AB⊥CD,
∴BC弧=BD弧,∠OED=90°,
∴∠BOD=∠COB,
∵∠D=30°,
∴∠DOE=∠AOF=∠BOC=60°,
∴∠COF=60°,
∴∠COF=∠COB=60°,
∴![]() =
=![]() .
.
(2)∵OC=OF,∠COF=60°
∴△COF是等边三角形,
∴∠OFC=60°,
∵∠G=30°,∠OFC=∠G+∠FCG,
∴∠FCG=30°,
∴∠G=∠FCG,
∴GF=CF,
∵DF是直径,
∴∠FCD=90°,
∵∠D=30°,CD=6,DF=2CF,设CF=a,则DF=2a
∴a2+36=4a2,
∵a>0,
∴a=2![]() ,
,
∴GF=CF=2![]() .
.

练习册系列答案
相关题目
【题目】某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
劳动时间(小时) | 3 | 3.5 | 4 | 4.5 |
人数 | 1 | 1 | 2 | 1 |
A.中位数是4,平均数是3.75
B.众数是4,平均数是3.8
C.众数是2,平均数是3.75
D.众数是2,平均数是3.8