题目内容
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
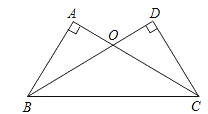
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)利用“HL”证明Rt△ABC和Rt△DCB全等,根据全等三角形对应边相等可得AB=DC,然后利用“角角边”证明△ABO和△DCO全等即可;
(2)根据全等三角形对应边相等可得AO=DO,然后求出OB=OC,再根据等腰三角形的定义解答.
试题解析:(1)在Rt△ABC和Rt△DCB中,
![]() ,
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=DC,
在△ABO和△DCO中,
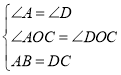 ,
,
∴△ABO≌△DCO(AAS);
(2)△OBC是等腰三角形.
理由如下:∵△ABO≌△DCO,
∴AO=DO,
∵AC=BD,
∴AC-AO=BD-DO,
即OB=OC,
∴△OBC是等腰三角形.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目