题目内容
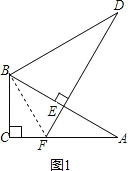
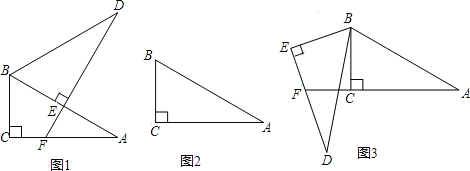
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
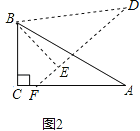
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
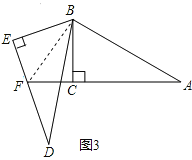
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
【答案】(1)证明见解析;(2)画图见解析,(1)中的结论AF+EF=DE仍然成立;(3)不成立,AF= DE+EF.
【解析】
试题分析:(1)我们已知了三角形BED和CAB全等,那么DE=AF+CF,因此只要求出EF=CF就能得出本题所求的结论,可通过全等三角形来实现,连接BF,那么证明三角形BEF和BCF全等就是解题的关键,这两三角形中已知的条件有BE=BC,一条公共边,根据斜边直角边定理,这两个直角三角形就全等了,也就得出EF=CF,也就能证得本题的结论了;
(2)解题思路和辅助线的作法与(1)完全一样;
(3)同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.
(1)证明:连接BF(如图①),
∵△ABC≌△DBE(已知),
∴BC=BE,AC=DE.
∵∠ACB=∠DEB=90°,
∴∠BCF=∠BEF=90°.
∵BF=BF,
∴Rt△BFC≌Rt△BFE.
∴CF=EF.
又∵AF+CF=AC,
∴AF+EF=DE.
(2)解:画出正确图形如图②
∴(1)中的结论AF+EF=DE仍然成立;
(3)不成立.
证明:连接BF,
∵△ABC≌△DBE,
∴BC=BE,
∵∠ACB=∠DEB=90°,
∴△BCF和△BEF是直角三角形,
在Rt△BCF和Rt△BEF中,
![]() ,
,
∴△BCF≌△BEF(HL),
∴CF=EF;
∵△ABC≌△DBE,
∴AC=DE,
∴AF=AC+FC=DE+EF.