题目内容
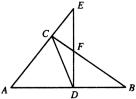
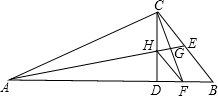 已知如图,CD是RT△ABC斜边上的高,∠A的平分线交CD于H,交∠BCD的平分线于G,
已知如图,CD是RT△ABC斜边上的高,∠A的平分线交CD于H,交∠BCD的平分线于G,
求证:HF∥BC.
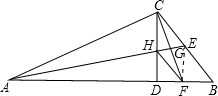 证明:连接FE,
证明:连接FE,∵CD是Rt△ABC斜边上的高,
∴∠A=∠DCB,
又∵AE平分∠A,CF平分∠BCD,
∴∠DCF=∠DAE,
又∵∠AHD=∠CHE,∠ADH=90度,
∴∠CGE=90度,
在三角形ACF中,AE是高,中线,角平分线,
∴CF⊥HE,CG=FG,
∴CH=FH,CE=EF,
∴CF是△CHE的高,中线,角平分线,
∴CH=CE,
∴CH=HF=EF=CE,
∴四边形HCEF是菱形,
∴HF∥BC.
分析:根据角平分线性质作辅助线连接FE,进而证得HCEF是菱形从而证得.
点评:本题考查了角平分线性质以及其应用,问题有一定难度.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
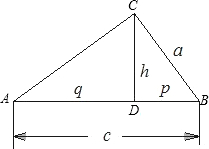 已知:如图,CD是Rt△ABC的斜边AB上的高,且BC=a,AB=c,CD=h,AD=q,DB=p.求证:h2=p•q,a2=p•c.
已知:如图,CD是Rt△ABC的斜边AB上的高,且BC=a,AB=c,CD=h,AD=q,DB=p.求证:h2=p•q,a2=p•c.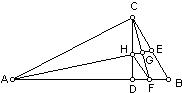 5、已知如图,CD是RT△ABC斜边上的高,∠A的平分线交CD于H,交∠BCD的平分线于G,
5、已知如图,CD是RT△ABC斜边上的高,∠A的平分线交CD于H,交∠BCD的平分线于G,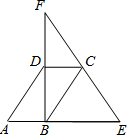 已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,AD∥BC.
已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,AD∥BC.