题目内容
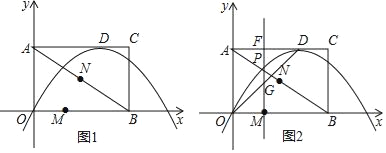
【题目】如图所示,在平面直角坐标系中,矩形AOBC的两边与坐标轴重合,且OB=4,AO=3,若AD=3DC,以D为顶点的抛物线过原点.点M、N为动点,设运动时间为t秒.
(1)求抛物线的解析式;
(2)在图1中,若点M在线段OB上从点O向点B以1个单位/秒的速度运动,同时,点N在线段BA上从点B向点A以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△BMN为直角三角形?
(3)在图2中,过点M做y轴的平行线,分别交抛物线和线段OD于P、G两点,当t为何值时,△ODP的面积最大?最大值是多少?
【答案】(1)y=﹣![]() x2+2x;(2)当t=
x2+2x;(2)当t=![]() 或t=
或t=![]() 时,△BMN为直角三角形;(3)当t=
时,△BMN为直角三角形;(3)当t=![]() 时,△OPD的面积最大,最大值为
时,△OPD的面积最大,最大值为![]()
【解析】分析:(1)求出点D的坐标,再利用顶点坐标式求出抛物线的解析式;
(2)分∠NMB=90°时,△AOB∽△NMB和当∠MNB=90°时,得到△AOB∽△MNB两种情况进行讨论,求出t的值即可;
(3)首先求出直线OD的解析式,再用t表示出PG的长,用t表示出△OPD的面积,进而求出最大值.
详解:(1)由题意,知AC=4,AD=3CD,得D点坐标为(3,3),根据顶点式设抛物线的解析式为y=a(x﹣3)2+3,
将点O坐标代入即可求出a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+2x;
x2+2x;
(2)依题意得,OA=3,OB=4,
∴AB=5,
∵OM=t,故得BM=(4﹣t),BN=2t,
①当∠NMB=90°时,得到△AOB∽△NMB,
得到![]() =
=![]() ,得
,得![]() =
=![]() ,解得t=
,解得t=![]() ;
;
②当∠MNB=90°时,得到△AOB∽△MNB,
得![]() =
=![]() ,得
,得![]() =
=![]() ,解得t=
,解得t=![]() ,
,
∴当t=![]() 或t=
或t=![]() 时,△BMN为直角三角形;
时,△BMN为直角三角形;
(3)∵O(0,0),D(3,3),
∴设直线OD的解析式为y=kx,则3k=3,k=1,
故直线OD的解析式为y=x,
∵OM=t,故xM=xG=xF=t,
∴yP=﹣![]() t2+2t,yG=t,
t2+2t,yG=t,
∴PG=﹣![]() t2+t,
t2+t,
∴S△OPD=![]() ADFG=﹣
ADFG=﹣![]() t2+
t2+![]() t,
t,
∴S△OPD=![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<
(0<t<![]() ),
),
∴当t=![]() 时,△OPD的面积最大,最大值为
时,△OPD的面积最大,最大值为![]() .
.

【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人.
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.