题目内容
【题目】在平面直角坐标系xOy中,已知点B(8,0)和点C(9, ![]() ).抛物线
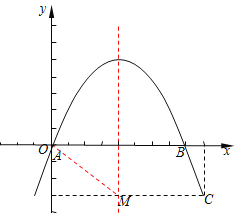
).抛物线![]() (a,c是常数,a≠0)经过点B、C,且与x轴的另一交点为A.对称轴上有一点M ,满足MA=MC.
(a,c是常数,a≠0)经过点B、C,且与x轴的另一交点为A.对称轴上有一点M ,满足MA=MC.
(1)求这条抛物线的表达式;
(2)求四边形ABCM的面积;
(3)如果坐标系内有一点D,满足四边形ABCD是等腰梯形,且AD//BC,求点D的坐标.
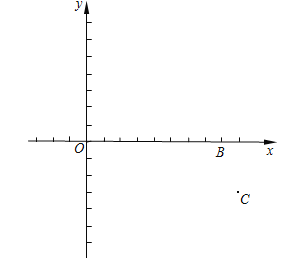
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(
;(3)(![]() ,
, ![]() )
)
【解析】试题分析:(1)根据抛物线的解析式,求得抛物线的对称轴,根据抛物线的对称性求得点A的坐标,再将A、C的坐标代入函数解析式,求得a、c的值,即可求得这条抛物线的表达式;(2)因点M在对称轴上,设M(4,y),由MA=MC,即![]() ,根据勾股定理列出方程
,根据勾股定理列出方程![]() ,解得y=-3,即可得M(4,-3),再由四边形ABCM为梯形,根据梯形的面积公式即可求得四边形ABCM的面积;(3)用待定系数法求得直线BC的解析式,因AD//BC,即可求得直线AD的解析式,设D(x,-3x),根据勾股定理得方程
,解得y=-3,即可得M(4,-3),再由四边形ABCM为梯形,根据梯形的面积公式即可求得四边形ABCM的面积;(3)用待定系数法求得直线BC的解析式,因AD//BC,即可求得直线AD的解析式,设D(x,-3x),根据勾股定理得方程![]() 解得x的值,即可求得点D的坐标.
解得x的值,即可求得点D的坐标.
试题解析:
(1)由题意得:抛物线对称轴![]() ,即
,即![]() .
.
点B(8,0)关于对称轴的对称点为点A(0,0)∴![]() ,将C(9,-3)代入
,将C(9,-3)代入![]() ,得
,得![]()
∴抛物线的表达式:![]()
(2)∵点M在对称轴上,∴可设M(4,y)
又∵MA=MC,即![]()
∴![]() ,解得y=-3,∴M(4,-3)
,解得y=-3,∴M(4,-3)
∵MC//AB且MC≠AB,∴四边形ABCM为梯形,,AB=8,MC=5,AB边上的高h=yM=3
∴![]()
(3)将点B(8,0)和点C(9,﹣3)代入![]() 可得
可得
![]() ,解得
,解得![]()
由题意得.∵AD//BC,![]() ∴
∴![]() ,
,![]()
又∵AD过(0,0),DC=AB=8,设D(x,-3x),
![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴![]() ,
,
∴点D的坐标![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目