题目内容
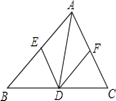
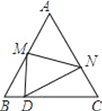
【题目】如图,等边△ABC中,D是边BC上的一点,且BD:DC=3:5,把△ABC折叠,使点A落在边BC上的点D处,若AM=5,那么AN的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:由BD:DC=3:5,可设BD=3a,则CD=5a,根据等边三角形的性质和折叠的性质可得:BM+MD+BD=5a,DN+NC+DC=11a,再通过证明△BMD∽△CDN即可求得AM:AN的值,即可求得AN的长.
详解:∵BD:DC=3:5,
∴设BD=3a,则CD=5a,
∵△ABC是等边三角形,
∴AB=BC=AC=8a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=5a,DN+NC+DC=7a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MBD=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=AM:AN,
即AM:AN=11:13,
∵AM=5,
∴AN=![]() .
.
故选:D.

练习册系列答案
相关题目