Question

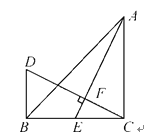
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC，AE为BC边上的中线，过点C作CF⊥AE，垂足为点F，在直线CF上截取CD＝AE.

(1)求证：BD⊥BC；

(2)若AC＝12 cm，求BD的长．

Answer 1

【答案】(1)证明见解析；(2) BD＝6 cm.

【解析】

（1）由∠ACB＝90°，CF⊥AE于点F易证∠EAC=∠BCD，这样结合AC=BC，AE=CD即可证得△AEC≌△CDB，从而可得∠DBC=∠ACE=90°，由此即可得到BD⊥BC；

（2）由AC=BC，AC=12cm可得BC=12cm，结合AE是△ABC的中线可得CE=6cm，这样由（1）中所得△AEC≌△CDB即可得到BD=CE=6cm.

(1)∵在△ABC中，∠ACB＝90°，

∴∠EAC＋∠AEC＝90°，

∵CF⊥AE，

∴∠BCD＋∠AEC＝90°，∴∠EAC＝∠BCD.

在△AEC和△CDB中，，

∴△AEC≌△CDB(SAS)，

∴∠DBC＝∠ACE＝90°，

∴BD⊥BC；

(2)∵AC=BC，AC=12cm，

∴BC=12cm，

∵AE是BC边上的中线，

∴CE＝BC＝6cm，

∵△AEC≌△CDB，

∴BD＝CE=6 cm.