题目内容
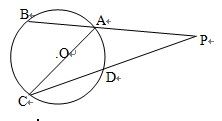
如图,⊙O是Rt ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E.
ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E.

(1)求证:∠BCA=∠BAD;
(2)求DE的长.
 ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E.
ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E.
(1)求证:∠BCA=∠BAD;
(2)求DE的长.
(1)证明见解析;(2) .
.
 .
.试题分析:(1)根据BD=BA得出∠BDA=∠BAD,再由∠BCA=∠BDA即可得出结论;
(2)判断△BED∽△CBA,利用对应边成比例的性质可求出DE的长度.
试题解析:(1)∵∠BCA=∠BDA,
∵BD=BA,
∴∠BAD=∠BDA,
∴∠BCA=∠BAD.
(2)在Rt
 ABC中,∠ABC=90°,AC=13,BC=5,
ABC中,∠ABC=90°,AC=13,BC=5,∴
 ,
,∵BE⊥DC,∴∠E=90°,
∵∠EDB=∠BAC.
∴△DEB∽△ABC,
∴
 ,
,∴
 .
.考点: 1.切线的判定;2.圆周角定理;3.相似三角形的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

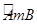 上任两点,则∠C+∠D的度数是_____°.
上任两点,则∠C+∠D的度数是_____°.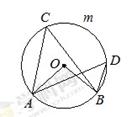
 cm2
cm2 cm2
cm2 cm2
cm2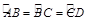 ,BA和CD的延长线相交于P,∠P=40°,则∠ACD的度数是( )
,BA和CD的延长线相交于P,∠P=40°,则∠ACD的度数是( )