题目内容
【题目】已知,抛物线y=x2+2mx(m为常数且m≠0).
(1)判断该抛物线与x轴的交点个数,并说明理由.
(2)若点A(-n+5,0),B(n-1,0)在该抛物线上,点M为抛物线的顶点,求△ABM的面积.
(3)若点(2,p),(3,g),(4,r)均在该抛物线上,且p<g<r,求m的取值范围.
【答案】(1)抛物线与x轴有2个交点,理由见解析;(2)△ABM的面积为8;(3)m的取值范围m>-2.5
【解析】
(1)首先算出根的判别式b2-4ac的值,根据偶数次幂的非负性,判断该值一定大于0,从而根据抛物线与x轴交点个数与根的判别式的关系即可得出结论;
(2)根据抛物线的对称性及A,B两点的坐标特点求出抛物线的对称轴直线为x=2.从而再根据抛物线对称轴直线公式建立方程,求解算出m的值,进而求出抛物线的解析式,得出A,B,M三点的坐标,根据三角形的面积计算方法,即可算出答案;
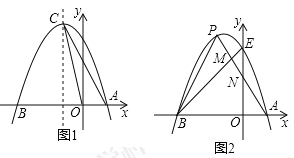
(3)方法一(图象法):根据抛物线的对称轴直线及开口方向判断出当对称轴在直线x=3的右边时,显然不符合题目条件;当对称轴在直线x=2的左边时,显然符合题目条件(如图2),从而列出不等式得出m的取值范围;当对称轴在直线x=2和x=3之间时,满足3-(-m)>-m-2即可(如图3),再列出不等式得出m的取值范围,综上所述,求出m的取值范围;方法二(代数法):将三点的横坐标分贝代入抛物线的解析式,用含m的式子表示出p,g,r,再代入 p<g<r 即可列出关于m的不等式组,求解即可。
(1)解:抛物线与x轴有2个交点。理由如下:
∵m≠0,∴b2-4ac =(2m)2-4×1×0=4m2>0.
∴抛物线与x轴有2个交点
(2)解:∵点A(-n+5,0),B(n-1,0)在抛物线上
∴抛物线的对称轴x=![]()
∴ ![]() =2,即m=-2.
=2,即m=-2.
∴抛物线的表达式为y=x2-4x.
∴点A(0,0),点B(4,0)或点A(4,0),点B(0,0),点M(2,-4)
∴△ABM的面积为![]() ×4×4=8
×4×4=8
(3)解:方法一(图象法):
∵抛物线y=x2+2mx的对称轴为x=-m,开口向上。
∴当对称轴在直线x=3的右边时,显然不符合题目条件(如图1).
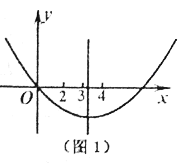
当对称轴在直线x=2的左边时,显然符合题目条件(如图2).
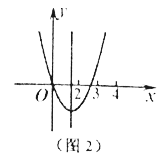
此时,-m<2,即m>-2.
当对称轴在直线x=2和x=3之间时,满足3-(-m)>-m-2即可(如图3).
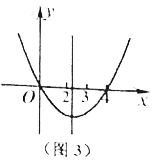
即m>-2.5.
综上所述,m的取值范围m>-2.5
方法二(代数法):
由已知得,p=4+4m,g=9+6m,r=16+8m.
∵p<q<r, ∴4+4m<9+6m<16+8m,解得m>-2.5.